
丂恾侾丂堎側傞僲僀僘儗儀儖偱嶣塭偝傟偨價乕僘嬍偺X慄幨恀丏
丂嵍丗僲僀僘儗儀儖偑掅偄乮棻忬惈偑椙偄丏恾俀偺嘆偺忬懺乯丏塃丗僲僀僘儗儀儖偑崅偄乮棻忬惈偑埆偄丏恾俀偺嘇偺忬懺乯丏
丂夋憸恌抐偱偼丆彫偝偔偰掅僐儞僩儔僗僩側怣崋傕梕堈偵幆暿偱偒傞傛偆側夋幙傪傕偭偨夋憸傪採嫙偡傞偙偲偑戝愗偱偁傞丏
係丏倂俽偺應掕丂
亂僲僀僘摿惈亃
僲僀僘摿惈偺暅廗丒妋擣丏憹姶巻亅僼傿儖儉宯偺応崌丆堦條偵X慄傪徠幩偟偰摼傜傟偨X慄僼傿儖儉忋偺崟壔嬧偺暘晍偼堦條偱偼側偄丏夋憸傪拲堄怺偔挱傔傞偲丆崟壔嬧偺廤傑傝乮mottle丗儌僩儖乯偑晄婯懃偵曄壔偡傞柾條偲偟偰娤嶡偱偒傞丏偦偺堦椺偲偟偰丆恾侾偵價乕僘嬍偺X慄幨恀傪帵偡丏

丂恾侾丂堎側傞僲僀僘儗儀儖偱嶣塭偝傟偨價乕僘嬍偺X慄幨恀丏
丂嵍丗僲僀僘儗儀儖偑掅偄乮棻忬惈偑椙偄丏恾俀偺嘆偺忬懺乯丏塃丗僲僀僘儗儀儖偑崅偄乮棻忬惈偑埆偄丏恾俀偺嘇偺忬懺乯丏
丂夋憸恌抐偱偼丆彫偝偔偰掅僐儞僩儔僗僩側怣崋傕梕堈偵幆暿偱偒傞傛偆側夋幙傪傕偭偨夋憸傪採嫙偡傞偙偲偑戝愗偱偁傞丏
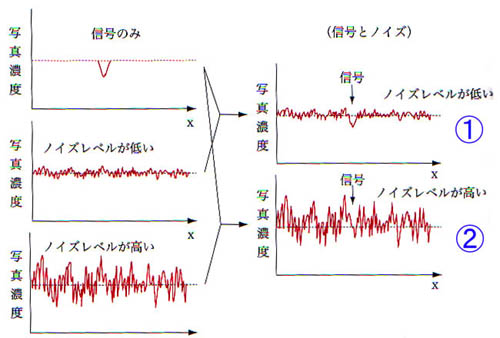
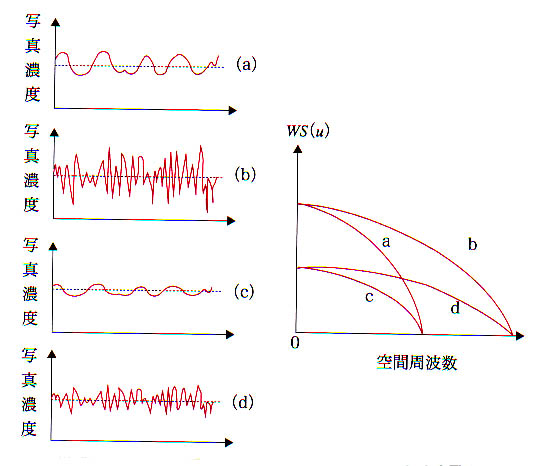
丂恾俀丂旝彫偱掅僐儞僩儔僗僩側怣崋偲夋憸偺僲僀僘儗儀儖
偙偺傛偆側夋憸偺僓儔僣僉傪棻忬偲偄偄丆棻忬偺帵偡惈幙傪棻忬惈偁傞偄偼僲僀僘摿惈偲偄偆丏僲僀僘摿惈偼丆RMS棻忬搙乮root
mean square乯傗僂傿乕僫乕僗儁僋僩儖乮WS丗Wiener spectrum乯乵僲僀僘僷儚乕僗儁僋僩儖乮NPS丗noise
power spectrum乯偲傕屇偽傟傞乶偱昡壙偡傞偙偲偑偱偒傞丏棻忬偺庡偨傞尨場偼丆X慄偑憹姶巻亅僼傿儖儉宯偱媧廂偝傟傞尰徾偑儔儞僟儉側偨傔偱偁傞丏X慄岝巕偺儔儞僟儉側尰徾偺寢壥偲偟偰丆X慄岝巕偑媧廂偝傟傞埵抲傗枾搙偼摑寁揑側備傜偓傪傕偮丏X慄岝巕偺備傜偓偺摑寁揑側暘晍偼Poisson暘晍偵廬偄丆
![]()
偱昞傢偝傟傞丏N偼扨埵柺愊摉偨傝偵媧廂偝傟偨暯嬒偺X慄岝巕偺屄悢丆冃偼X慄岝巕偺曄摦傪帵偡昗弨曃嵎偱偁傞丏椺偊偽丆憹姶巻亅僼傿儖儉宯偱幨恀擹搙1.0傪摼傞偲偒丆扨埵柺愊乮![]() )摉偨傝偵媧廂偝傟偨暯嬒偺X慄岝巕悢偑10000屄偱偁偭偨偲壖掕偡傞偲丆0.1
)摉偨傝偵媧廂偝傟偨暯嬒偺X慄岝巕悢偑10000屄偱偁偭偨偲壖掕偡傞偲丆0.1![]() 偺旕忢偵彫偝側柺愊偵偼暯嬒100屄偺X慄岝巕偑媧廂偝傟偨偙偲偵側傞丏偟偐偟丆偙偺彫偝側柺愊偵媧廂偝傟偨暯嬒偺X慄岝巕悢偵懳偡傞昗弨曃嵎傪寁嶼偡傞偲丆
偺旕忢偵彫偝側柺愊偵偼暯嬒100屄偺X慄岝巕偑媧廂偝傟偨偙偲偵側傞丏偟偐偟丆偙偺彫偝側柺愊偵媧廂偝傟偨暯嬒偺X慄岝巕悢偵懳偡傞昗弨曃嵎傪寁嶼偡傞偲丆
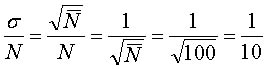
偲側傝丆摑寁揑偵偼10%傕備傜偄偱偄傞偙偲偑傢偐傞丏偮傑傝丆0.1![]() 偺柺愊偵偼丆忢偵100屄偺X慄岝巕偑傄偭偨傝媧廂偝傟傞偺偱偼側偔丆栺90乣110屄偺X慄岝巕偑媧廂偝傟傞偙偲傪堄枴偡傞丏偙偆偟偨X慄岝巕偺悢傗暘晍偑摑寁揑偵備傜偖偙偲偵婲場偡傞僲僀僘偼X慄検巕儌僩儖乮quantum
mottle乯偲傛偽傟丆憹姶巻亅僼傿儖儉宯偺僲僀僘亖X慄幨恀儌僩儖乮radiographic
mottle乯偺側偐偱嵟傕戝偒側妱崌乮60%埲忋乯傪愯傔偰偄傞丏恾俁偵憹姶巻亅僼傿儖儉宯偵傛傞X慄幨恀偺僲僀僘偺峔惉傪帵偡丏
偺柺愊偵偼丆忢偵100屄偺X慄岝巕偑傄偭偨傝媧廂偝傟傞偺偱偼側偔丆栺90乣110屄偺X慄岝巕偑媧廂偝傟傞偙偲傪堄枴偡傞丏偙偆偟偨X慄岝巕偺悢傗暘晍偑摑寁揑偵備傜偖偙偲偵婲場偡傞僲僀僘偼X慄検巕儌僩儖乮quantum
mottle乯偲傛偽傟丆憹姶巻亅僼傿儖儉宯偺僲僀僘亖X慄幨恀儌僩儖乮radiographic
mottle乯偺側偐偱嵟傕戝偒側妱崌乮60%埲忋乯傪愯傔偰偄傞丏恾俁偵憹姶巻亅僼傿儖儉宯偵傛傞X慄幨恀偺僲僀僘偺峔惉傪帵偡丏
丂恾俁丂憹姶巻亅僼傿儖儉宯偵傛傞X慄幨恀偺僲僀僘峔惉
憹姶巻偺峔憿儌僩儖乮structure mottle乯偼丆憹姶巻偺寀岝懱偺峔憿偺晄嬒堦惈偵娭學偡傞傕偺偱偁傞丏僼傿儖儉偺棻忬乮film graininess乯偼丆X慄僼傿儖儉帺懱偑傕偲傕偲傕偭偰偄傞棻忬偱偁傞丏傑偨丆X慄検巕儌僩儖偲憹姶巻偺峔憿儌僩儖偼丆憹姶巻偑敪岝偟丆X慄僼傿儖儉偵婰榐偝傟傞夁掱偱X慄幨恀儌僩儖偵塭嬁偡傞傕偺偱偁傝丆偙傟傜傪暪偣偰憹姶巻儌僩儖乮screen
mottle乯偲偄偆丏偨偩偟丆憹姶巻儌僩儖偵愯傔傞憹姶巻偺峔憿儌僩儖偺妱崌偼丆X慄検巕儌僩儖偲斾傋偰旕忢偵彮側偄丏偙傟偼愭偵傕弎傋偨傛偆偵丆X慄検巕儌僩儖偑X慄幨恀儌僩儖偺拞偱嵟傕戝偒側妱崌傪愯傔偰偄傞偐傜偱偁傞丏傑偨丆掅偄嬻娫廃攇悢椞堟偱偼丆X慄検巕儌僩儖偑嵟傕巟攝揑側僲僀僘偱偁傞堦曽丆X慄僼傿儖儉偺棻忬惈偼嬻娫廃攇悢偵埶懚偣偢傎傏堦掕偺抣傪帵偟丆崅偄嬻娫廃攇悢椞堟偱嵟傕巟攝揑側僲僀僘場巕偲側傞丏
恾係偵丆憹姶巻偲X慄僼傿儖儉傪枾拝偝偣偰嶣塭偟偨X慄幨恀丆偍傛傃丆憹姶巻偲X慄僼傿儖儉偺娫妘傪俆抜奒偵曄壔偝偣偰嶣塭偟偨X慄幨恀傪帵偡丏偡傋偰偺幨恀偼摨偠X慄岝巕悢偱嶣塭偝傟偰偄傞丏

丂恾係丂乮a乯憹姶巻偲X慄僼傿儖儉傪枾拝偝偣偰摼偨X慄幨恀丆乮b乯亅乮f乯憹姶巻偲X慄僼傿儖儉偺娫偵僗儁乕僗傪愝偗偰嶣塭偟偨X慄幨恀乮b丗僗儁乕僗=0.02mm丆c丗0.05mm丆d丗0.12mm丆e丗0.23mm丆f丗13.0mm乯
偙傟傜偺X慄幨恀傪娤嶡偡傞偲丆憹姶巻偲X慄僼傿儖儉偑枾拝偟偨偲偒乮a偺幨恀乯偵偼慹偔偰慛柧側棻忬偺條巕偑尒偊傞丏偟偐偟丆憹姶巻偲X慄僼傿儖儉偺娫妘偑戝偒偔側傞偵廬偭偰丆棻忬偺柾條偑傏偐偝傟丆傗偑偰丆崅偄嬻娫廃攇悢惉暘傪傕偭偨慛塻偱嵶偐側X慄僼傿儖儉偺棻忬偩偗偑娤嶡偱偒傞乮倖偺幨恀乯丏偙偺寢壥傛傝丆X慄幨恀儌僩儖偼丆憹姶巻偱X慄偑媧廂偝傟丆敪岝偟偨岝偑X慄僼傿儖儉偵業岝偝傟傞夁掱偱丆岝偺奼嶶偵傛傞塭嬁丆偡側傢偪丆憹姶巻偵傛傞儃働乮MTF乯偺塭嬁傪庴偗傞偙偲傪帵偟偰偄傞丏
X慄幨恀儌僩儖偺側偐偱嵟傕戝偒側妱崌傪愯傔傞X慄検巕儌僩儖偺僂傿乕僫乕僗儁僋僩儖乮WSq乯偼丆MTF偺傎偐偵傕丆僼傿儖儉摿惈嬋慄偺僌儔僕僃儞僩乮G乯偲丆扨埵柺愊摉偨傝偵媧廂偟偨暯嬒偺X慄岝巕悢乮n乯偺塭嬁傪庴偗傞偙偲傪峫椂偡傞偲丆師幃偺傛偆偵嬤師偱偒傞偙偲偑抦傜傟偰偄傞丏
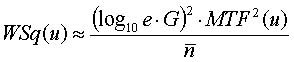
偙偺嬤師幃偼丆僲僀僘摿惈乮偙偺応崌偼X慄検巕儌僩儖乯偑丆夝憸摿惈傗擖弌椡摿惈偲偳偺傛偆側娭學傪傕偮偺偐傪棟夝偡傞偺偵栶棫偮丏偨偲偊偽丆X慄偵懳偡傞姶搙偼摨偠偱偁傞偑丆堎側偭偨夝憸摿惈乮MTF乯傪傕偭偨俀庬椶偺憹姶巻偲侾庬椶偺X慄僼傿儖儉傪慻傒崌傢偣偨俀偮偺僔僗僥儉傪峫偊傞丏偙偺偲偒n偲G偼摨偠偲偡傞偲丆X慄検巕儌僩儖偺僂傿乕僫乕僗儁僋僩儖偼丆夝憸摿惈偺桪傟偨乮MTF偑崅偄乯僔僗僥儉偺傎偆偑抣偑崅偔側傞偙偲偑棟夝偱偒傞丏摨條偵丆MTF偲値偑曄傢傜側偄偲壖掕偟偨応崌丆僼傿儖儉僐儞僩儔僗僩偺崅偄乮G偺抣偑戝偒偄乯僔僗僥儉偺傎偆偑僲僀僘儗儀儖偑崅偔側傞偙偲偑傢偐傞丏
僲僀僘摿惈偺昡壙偵偼丆RMS棻忬搙乮root mean square乯傗僂傿乕僫乕僗儁僋僩儖乮Wiener spectrum乯乵僲僀僘僷儚乕僗儁僋僩儖乮noise power spectrum乯偲傕屇偽傟傞乶偑梡偄傜傟偰偄傞丏媮傔曽傪娙扨偵傑偲傔傞偲師偺傛偆偵側傞丏

RMS棻忬搙偼嬶懱揑偵偼師偺幃偱媮傔傞偙偲偑偱偒傞丏N偼僨乕僞悢丆Di偼屄乆偺幨恀擹搙僨乕僞丆![]() 偼幨恀擹搙僨乕僞偺暯嬒抣偱偁傞丏
偼幨恀擹搙僨乕僞偺暯嬒抣偱偁傞丏
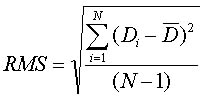
偙偺幃偼丆昗弨曃嵎偺幃偦偺傕偺偱偁傞丏昗弨曃嵎偼丆暯嬒抣偵懳偟偰抣偑偳偺掱搙曄摦偡傞偺偐傪帵偡傕偺偱丆暯嬒抣亇1冃乮冃亖RMS乯偺斖埻撪偵丆栺68%偺僨乕僞偑娷傑傟傞偙偲傪堄枴偡傞丏RMS偺抣偑戝偒偄傎偳丆曄摦偑戝偒偄偙偲傪帵偡偺偱丆棻忬惈偼埆偄丏RMS棻忬搙偼丆寁嶼偑娙扨偱桳梡偱偼偁傞偗傟偳丆僲僀僘摿惈偺堦晹傪昞傢偟偰偄傞偵夁偓側偄偨傔丆徻嵶側僲僀僘夝愅傪峴偆偙偲偼偱偒側偄丏堦曽丆僂傿乕僫乕僗儁僋僩儖偼丆嬻娫廃攇悢偺帇揰偐傜僲僀僘儗儀儖傪應掕偡傞偙偲偑偱偒丆傛傝徻嵶側僲僀僘夝愅偑壜擻偱偁傞丏僂傿乕僫乕僗儁僋僩儖傪媮傔傞曽朄偼丆幨恀擹搙僨乕僞偐傜帺屓憡娭娭悢乮ACF丗auto-correlation function乯傪媮傔偦傟傪僼乕儕僄曄姺偡傞曽朄偲丆幨恀擹搙僨乕僞傪捈愙僼乕儕僄曄姺偡傞曽朄偑偁傞丏帺屓憡娭娭悢偼師幃偱昞傢偝傟傞丏
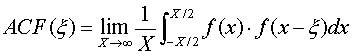
帺屓憡娭娭悢偼丆兲=0偱嵟戝偺抣傪偲傝丆憡娭嫍棧偑戝偒偔側傞偵偮傟偰彫偝側抣傪偲傞丏帺屓憡娭娭悢偺幃偼丆摨偠娭悢偺廳忯愊暘偱昞傢偝傟偰偄傞偙偲偐傜丆帺屓憡娭娭悢傪僼乕儕僄曄姺偡傞偲丆俀偮偺摨偠娭悢f(x)偺僼乕儕僄曄姺偺妡偗嶼丆偡側傢偪丆![]() 偑媮傑傞丏偙傟傪僲僀僘僷儚乕僗儁僋僩儖乮NPS乯偲偄偄丆夋憸偱偼丆僂傿乕僫乕僗儁僋僩儖偲屇傫偱偄傞丏偟偨偑偭偰丆媡偵丆僂傿乕僫乕僗儁僋僩儖傪媡僼乕儕僄曄姺偡傟偽帺屓憡娭娭悢偑媮傑傞丏傕偆堦曽偺幨恀擹搙僨乕僞傪捈愙僼乕儕僄曄姺偡傞曽朄偵偮偄偰偼偁偲偱徻嵶傪弎傋傞偲偟偰丆偙偙偱偼傑偢偼僂傿乕僫乕僗儁僋僩儖偺尒曽傗偦偺夝庍偵偮偄偰弎傋傞丏恾俆偵僂傿乕僫乕僗儁僋僩儖偺僌儔僼偺椺傪帵偡丏
偑媮傑傞丏偙傟傪僲僀僘僷儚乕僗儁僋僩儖乮NPS乯偲偄偄丆夋憸偱偼丆僂傿乕僫乕僗儁僋僩儖偲屇傫偱偄傞丏偟偨偑偭偰丆媡偵丆僂傿乕僫乕僗儁僋僩儖傪媡僼乕儕僄曄姺偡傟偽帺屓憡娭娭悢偑媮傑傞丏傕偆堦曽偺幨恀擹搙僨乕僞傪捈愙僼乕儕僄曄姺偡傞曽朄偵偮偄偰偼偁偲偱徻嵶傪弎傋傞偲偟偰丆偙偙偱偼傑偢偼僂傿乕僫乕僗儁僋僩儖偺尒曽傗偦偺夝庍偵偮偄偰弎傋傞丏恾俆偵僂傿乕僫乕僗儁僋僩儖偺僌儔僼偺椺傪帵偡丏
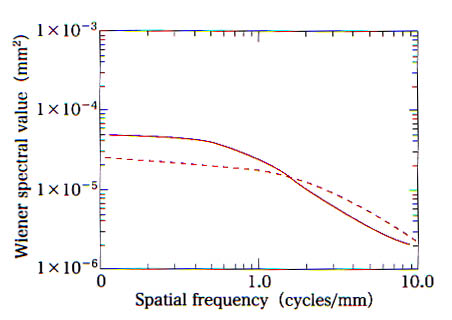
丂恾俆丂俀偮偺堎側傞僔僗僥儉偺僂傿乕僫乕僗儁僋僩儖
墶幉偼嬻娫廃攇悢乮cycles/mm乯偱偁傝丆廲幉偑僂傿乕僫乕僗儁僋僩儖偺抣乮![]() 乯傪帵偟偰偄傞丏僂傿乕僫乕僗儁僋僩儖偺僌儔僼偼丆椉懳悢偱僾儘僢僩偡傞偙偲偑懡偄丏恾俆傕廲幉丆墶幉偲傕偵懳悢偱昞帵偝傟偰偄傞丏偙偙偱拲堄偟偰傕傜偄偨偄偺偼丆僂傿乕僫乕僗儁僋僩儖偺扨埵偼mm偺擇忔偱昞傢偝傟傞柺愊偱偁傞偲偄偆偙偲両偦傟偱偼丆偁傞嬻娫廃攇悢偵偍偄偰僂傿乕僫乕僗儁僋僩儖偺抣偺戝彫偼壗傪堄枴偡傞偺偐丏僂傿乕僫乕僗儁僋僩儖偺抣偑戝偒偄偲偄偆偙偲偼丆僲僀僘偺儗儀儖偑崅偄乮棻忬惈偑埆偄亖僲僀僘偑懡偄乯偙偲傪堄枴偟偰偄傞丏恾俆偺椺偱傒傞偲丆1.0cycles/mm偁偨傝傑偱偺掅嬻娫廃攇悢堟偱偼丆揰慄偺僔僗僥儉偺傎偆偑幚慄偺僔僗僥儉偵斾傋偰僲僀僘惉暘偑彮側偄偲偄偊傞丏偝傜偵棟夝傪怺傔傞偨傔偵丆恾俇偵係偮偺堎側傞幨恀擹搙偺暘晍偲丆偦傟傜偺僂傿乕僫乕僗儁僋僩儖偺柾幃恾傪帵偡丏恾俇偺偙偺娭學恾偼昁偢妎偊偰偍偙偆両
乯傪帵偟偰偄傞丏僂傿乕僫乕僗儁僋僩儖偺僌儔僼偼丆椉懳悢偱僾儘僢僩偡傞偙偲偑懡偄丏恾俆傕廲幉丆墶幉偲傕偵懳悢偱昞帵偝傟偰偄傞丏偙偙偱拲堄偟偰傕傜偄偨偄偺偼丆僂傿乕僫乕僗儁僋僩儖偺扨埵偼mm偺擇忔偱昞傢偝傟傞柺愊偱偁傞偲偄偆偙偲両偦傟偱偼丆偁傞嬻娫廃攇悢偵偍偄偰僂傿乕僫乕僗儁僋僩儖偺抣偺戝彫偼壗傪堄枴偡傞偺偐丏僂傿乕僫乕僗儁僋僩儖偺抣偑戝偒偄偲偄偆偙偲偼丆僲僀僘偺儗儀儖偑崅偄乮棻忬惈偑埆偄亖僲僀僘偑懡偄乯偙偲傪堄枴偟偰偄傞丏恾俆偺椺偱傒傞偲丆1.0cycles/mm偁偨傝傑偱偺掅嬻娫廃攇悢堟偱偼丆揰慄偺僔僗僥儉偺傎偆偑幚慄偺僔僗僥儉偵斾傋偰僲僀僘惉暘偑彮側偄偲偄偊傞丏偝傜偵棟夝傪怺傔傞偨傔偵丆恾俇偵係偮偺堎側傞幨恀擹搙偺暘晍偲丆偦傟傜偺僂傿乕僫乕僗儁僋僩儖偺柾幃恾傪帵偡丏恾俇偺偙偺娭學恾偼昁偢妎偊偰偍偙偆両
丂恾俇丂僂傿乕僫乕僗儁僋僩儖偵傛傞僲僀僘惉暘偺柾幃恾
乮a乯偲乮c乯偼斾妑揑掅偄嬻娫廃攇悢惉暘傪傕偪丆幨恀擹搙偺曄摦偑戝偒側乮a乯偺傎偆偑僂傿乕僫乕僗儁僋僩儖偺抣偑崅偄丏傑偨乮b乯偲乮d乯偼丆乮a乯偲乮c乯傛傝崅偄嬻娫廃攇悢偺惉暘傪傕偮偙偲傪帵偟丆幨恀擹搙偺曄摦偑戝偒側乮b乯偺傎偆偑僂傿乕僫乕僗儁僋僩儖偺抣偑崅偄丏偙偙偱丆RMS棻忬搙偲僂傿乕僫乕僗儁僋僩儖WS乮u乯偺娫偵偼丆
![]()
偺娭學偑偁傝丆僂傿乕僫乕僗儁僋僩儖偺柺愊偑丆RMS棻忬搙偺擇忔偵懳墳偡傞偙偲偑抦傜傟偰偄傞丏偙偺娭學偼丆偨偲偊RMS棻忬搙偑摨偠偱傕丆僂傿乕僫乕僗儁僋僩儖偼堎側偭偨條巕傪帵偡偙偲偑偁傞偙偲傪堄枴偡傞丏椺偊偽丆恾俇偵偍偄偰丆乮a乯偲乮d乯偱僂傿乕僫乕僗儁僋僩儖偺柺愊偑摨偠偱偁傞偲偡傞偲丆堎側傞僂傿乕僫乕僗儁僋僩儖傪帵偡偵傕偐偐傢傜偢丆RMS棻忬搙偼傑偭偨偔摨偠抣偲寁嶼偝傟偰偟傑偆丏偙傟偼丆RMS棻忬搙偱偼丆僲僀僘摿惈偺偡傋偰昞傢偡偙偲偼偱偒側偄偙偲傪柧帵揑偵帵偟偰偄傞丏偟偨偑偭偰丆夋憸偺僲僀僘摿惈傪徻嵶偵挷傋傞偨傔偵偼丆RMS棻忬搙偩偗偱偼廫暘偱側偔丆僂傿乕僫乕僗儁僋僩儖偺應掕偑昁梫偐偮廳梫偲側傞丏
偝偰丆偙偙偐傜偼僨傿僕僞儖X慄夋憸僔僗僥儉偺僲僀僘摿惈昡壙偵偮偄偰弎傋傞丏
僨傿僕僞儖X慄夋憸僔僗僥儉偵偍偗傞僲僀僘偺昡壙曽朄傕丆憹姶巻亅僼傿儖儉宯偲摨條偵丆RMS棻忬搙偵傛傞娙曋側曽朄偲丆僂傿乕僫乕僗儁僋僩儖傪梡偄偨曽朄偺椉曽傪偦偺傑傑巊偆偙偲偑偱偒傞丏偨偩丆僔僗僥儉偱敪惗偡傞僲僀僘偺峔惉側偳僨傿僕僞儖宯側傜偱偼傕偺偑偁傞偺偱丆傑偢偦傟傜偵偮偄偰娙扨偵弎傋偨屻偵丆嬶懱揑偵僨傿僕僞儖X慄夋憸僔僗僥儉偱偺僂傿乕僫乕僗儁僋僩儖偺應掕庤弴偵恑傓丏恾俈偼丆僨傿僕僞儖X慄夋憸僔僗僥儉偲偟偰CR僔僗僥儉偺偍傕側僲僀僘偺梫場傪傑偲傔偨傕偺偱偁傞丏
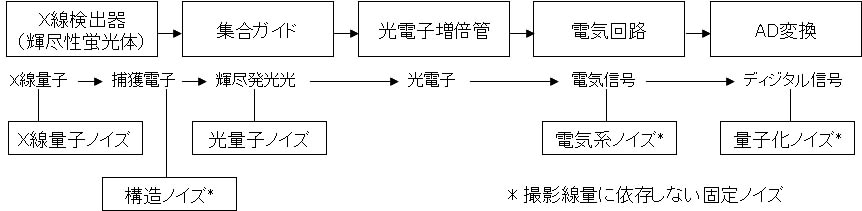
丂恾俈丂CR僔僗僥儉偺偍傕側僲僀僘峔惉
僨傿僕僞儖X慄夋憸僔僗僥儉偺峔惉偼憹姶巻亅僼傿儖儉宯偲斾傋偰暋嶨偱偁傝丆僲僀僘偺庡偨傞尨場偱偁傞X慄検巕儌僩儖偺傎偐偵傕丆X慄専弌婍偺峔憿僲僀僘乮偙偺椺偱偼僀儊乕僕儞僌僾儗乕僩偺峔憿僲僀僘乯丆婸恠敪岝偺岝検巕僲僀僘丆揹婥宯僲僀僘丆検巕壔僲僀僘側偳懡偔偺場巕偑偁傞丏偙傟傜偺拞偱丆峔憿僲僀僘丆揹婥宯僲僀僘丆検巕壔僲僀僘偼丆嶣塭慄検偵埶懚偣偢堦掕偺抣傪帵偡偨傔屌掕僲僀僘偲屇偽傟偰偄傞丏偝傜偵僔僗僥儉慡懱偺僲僀僘摿惈偵偼夋憸昞帵晹偺僲僀僘傕晅壛偝傟傞丏僨傿僕僞儖X慄僔僗僥儉偱偼丆旐敇慄検寉尭偺娤揰偐傜嶣塭慄検傪僐儞僩儘乕儖偟偰巊梡偡傞偨傔丆僨傿僕僞儖X慄僔僗僥儉偱傕X慄検巕儌僩儖偑巟攝揑偱偁傞偙偲偼憹姶巻亅僼傿儖儉宯偲曄傢傜側偄丏堦曽丆崅慄検堟偱偼X慄専弌婍偺峔憿僲僀僘偑巟攝揑偱偁傝丆偙偺椞堟偱偼嶣塭慄検傪憹壛偝偣偰傕僲僀僘摿惈偼夵慞偝傟側偄偺偱拲堄偑昁梫偱偁傞丏偙偺傎偐偵傕丆夋憸張棟偵傛偭偰僲僀僘摿惈偑夵慞偟偨傝丆媡偵僲僀僘偑憹壛偡傞偙偲傕偁傞丏師幃偼丆僨傿僕僞儖X慄夋憸僔僗僥儉偺憤崌揑側擇師尦偺僂傿乕僫乕僗儁僋僩儖乵僆乕僶乕僆乕儖僂傿乕僫乕僗儁僋僩儖丆WSoverall乮u丆v乯乶傪帵偟偨傕偺偱偁傞丏
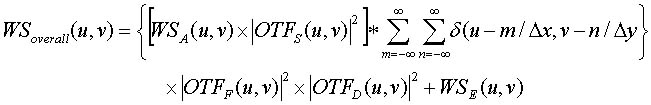
WSA乮u丆v乯偼傾僫儘僌惉暘偺僂傿乕僫乕僗儁僋僩儖偱丆捠忢丆X慄検巕儌僩儖偑戝偒側妱崌傪帵偡丏OTFS乮u丆v乯丆OTFF乮u丆v乯丆OTFD乮u丆v乯偼丆偦傟偧傟僒儞僾儕儞僌傾僷乕僠儍丆夋憸張棟僼傿儖僞丆僨傿僗僾儗僀傾僷乕僠儍偺儗僗億儞僗娭悢偱偁傞丏WSE乮u丆v乯偼丆夋憸弌椡晹偺晅壛僲僀僘偱偁傞丏乷丂乸撪偑僨傿僕僞儖僂傿乕僫乕僗儁僋僩儖偱偁傝丆乵丂乶撪偑僾儕僒儞僾儕儞僌僂傿乕僫乕僗儁僋僩儖偱偁傞丏僄儕傾僔儞僌僄儔乕偺岠壥偑柍帇偱偒傞応崌偵偼丆僾儕僒儞僾儕儞僌僂傿乕僫乕僗儁僋僩儖偲僨傿僕僞儖僂傿乕僫乕僗儁僋僩儖偼摍偟偔側傞丏幚嵺偵偼丆WSA乮u丆v乯偵OTFS乮u丆v乯偺擇忔偑妡偐偭偰偄傞偨傔丆偙傟傜偺僗儁僋僩儖偼傎傏摍偟偔側傞偲峫偊傜傟丆僨傿僕僞儖宯偺僲僀僘夝愅偵偼僨傿僕僞儖僂傿乕僫乕僗儁僋僩儖偑桳梡偲側傞丏偝傜偵僆乕僶乕僆乕儖僂傿乕僫乕僗儁僋僩儖偵偼丆OTFF乮u丆v乯偺擇忔偲OTFD乮u丆v乯偺擇忔偑妡偐偭偰偔傞偺偱丆崅偄嬻娫廃攇悢堟偵偍偗傞僄儕傾僔儞僌偺塭嬁偼傎偲傫偳柍帇偱偒傞偔傜偄偵彫偝偔側傞丏偙偺傛偆側応崌偵偼丆MTF偲偼堎側傝丆僆乕僶乕僆乕儖僂傿乕僫乕僗儁僋僩儖傕僲僀僘偺夝愅偵桳岠偲側傞丏
僨傿僕僞儖僂傿乕僫乕僗儁僋僩儖偺應掕偵偼嬒堦偵X慄徠幩傪峴偭偰摼傜傟偨僨傿僕僞儖X慄夋憸傪棙梡偡傞丏旐幨懱傪抲偐偢偵嶣塭偟丆偦偺偲偒偺慄検傪婰榐偟偰偍偔丏偙偆偟偨夋憸僨乕僞偐傜僨傿僕僞儖僂傿乕僫乕僗儁僋僩儖傪應掕偡傞曽朄偲偟偰丆壖憐僗儕僢僩朄偲擇師尦僼乕儕僄曄姺朄偑偁傞丏恾俉偵壖憐僗儕僢僩朄偺應掕庤弴丆恾俋偵擇師尦僼乕儕僄曄姺朄偺應掕庤弴傪帵偡丏
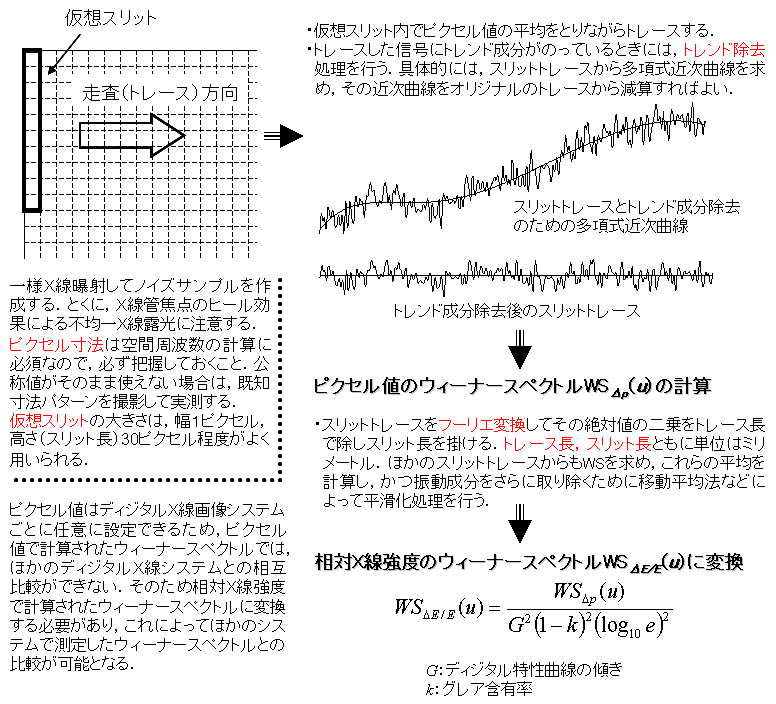
丂丂恾俉丂壖憐僗儕僢僩朄偵傛傞僂傿乕僫乕僗儁僋僩儖應掕偺奣棯
丂
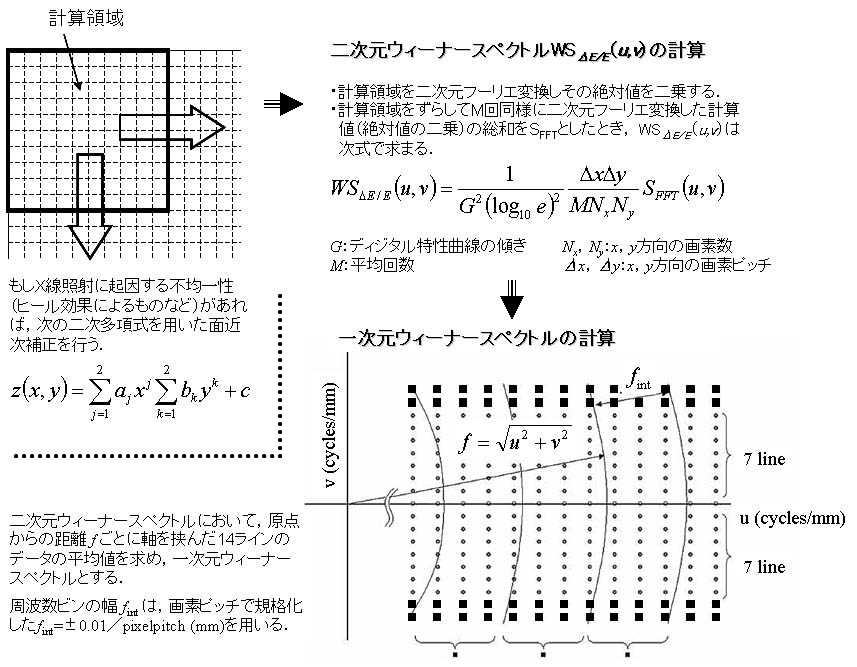
丂丂恾俋丂擇師尦僼乕儕僄曄姺朄偵傛傞僂傿乕僫乕僗儁僋僩儖應掕偺奣棯
丂
|
幚尡侾丗丂壖憐僗儕僢僩朄偱僨傿僕僞儖僂傿乕僫乕僗儁僋僩儖傪應掕偟偰傒傛偆 |
|
亂栚揑亃丂壖憐僗儕僢僩朄偵傛傞WS應掕朄傪廗摼偡傞丏 亂庤弴亃 侾丏僗儕僢僩僩儗乕僗僨乕僞偺庢摼
俀丏埲崀丆僩儗儞僪彍嫀張棟丆僩儗乕僗僨乕僞偺僼乕儕僄曄姺丆僺僋僙儖抣偺僂傿乕僫乕僗儁僋僩儖WS儮p嶼弌丆X慄嫮搙偺僂傿乕僫乕僗儁僋僩儖WS儮E/E傊偺曄姺傪弴偵Excel忋偱峴偆丏 A楍丗丂僩儗乕僗偺埵抲丂仺僩儗乕僗挿偼512僺僋僙儖側偺偱0乣511丏 *乯暋悢偺僗儕僢僩僩儗乕僗僨乕僞偐傜媮傔偨暋悢杮偺WS傪暯嬒偡傞偙偲偱應掕惛搙傪崅傔傞偙偲偑偱偒傞丏 僌儔僼偺嶌惉丗 亂峫嶡亃 |
|
幚尡俀丗丂夝憸摿惈偺堎側傞僲僀僘僒儞僾儖偱僂傿乕僫乕僗儁僋僩儖傪應掕偟偰傒傛偆丏 |
|
亂栚揑亃丂夝憸摿惈偲僲僀僘摿惈偺娭學傪棟夝偡傞丏 亂庤弴亃丂幚尡侾偲偼夝憸摿惈偺堎側傞僲僀僘僒儞僾儖偺夋憸僨乕僞乮Routine1435.raw丗1800亊1800僺僋僙儖丆2byte僨乕僞丆僒儞僾儕儞僌僺僢僠100兪m丆X慄憰抲丗搰捗惢嶌強丂UD150L亅30丆夋憸撉庢憰抲丗FCR丂XG亅1N丆娗揹埑丗42 kV丆娗揹棳帪娫愊丗2.8mAs丆徟揰僒僀僘丗彫徟揰丆FFD丗60cm丆晅壛僼傿儖僞丗0.5mm Al + 0.1mm Cu乯傪巊梡偡傞丏應掕庤弴偼丆幚尡侾偲摨偠丏 亂峫嶡亃 |
丂