図1 標本と母集団の関係
【概要】
ROC解析を行う目的は,”なにを評価するか” によって異なってくるが,その応用範囲は非常に広範囲に広がりつつある.
例えば,
①ある画像システム(CRなど)内のあるパラメータ(CRでのS値,L値など)を変えたときの病変検出能の効果判定,
②ある画像処理法を適用したときの有効性(診断能が向上するか否かなど)の判定,
③コンピュータ支援診断の性能評価,
④特定疾患についてのモダリティ別の診断能の比較,
などが挙げられる.
このようなROCによる評価は基本的には人間(医師?)の主観的な判断に基づく評価である.
そのため,同じ評価対象を同じ環境のもとで評価したとしても,評価結果は必ずしも再現されるとは限らない.
つまり,ROCの評価結果は本質的にバラツキをもったデータである.
そのため,ROCの評価では統計的な解析(統計的有意差検定)が必要不可欠となる.
ROC曲線間での統計的有意差検定について述べる前に,まず,予備知識として統計量の分布や推定,検定の考え方について少し解説する.
(少しと言いながら結構長く...)
◆統計量の分布
アンケートなどで得られる資料は,考えている対象全体からではなく,適当な小集団から得られるのが通常である.
例えば,ニュースでときどき流れる世論調査については,国民全員から調査アンケートを集めるわけではない.
適当に選んだ一部の人(数百~数千?)たちのアンケートを集計し,その動向を世論としているのだ.
このように,考えている対象全体を母集団をいい,適当に選んだ一部の集団を標本という.
世論調査の例では,国民全体が母集団,実際に世論調査のために選ばれた一部の人たちが標本に当たる.
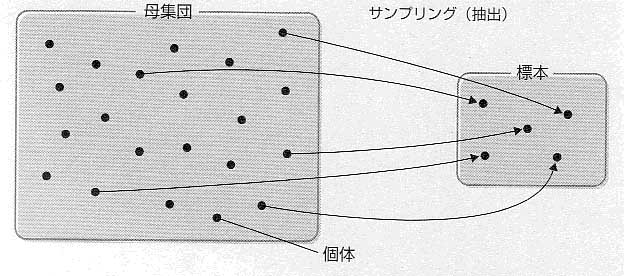
母集団から標本を選ぶことをサンプリング(抽出)と呼び,標本を構成するひとつひとつを個体と呼ぶ.そして,その個体数を標本の大きさという(図1).

図1 標本と母集団の関係
(注)母集団から標本を「適当」に選ぶと書いたが,この「適当」が難しい.資料の価値は,この選び方で決定されてしまう.
図2を見てみよう.この資料は,ある販売会社のたくさんの営業所の中から,8つの営業所をサンプリングし,その調査から得られたデータである.
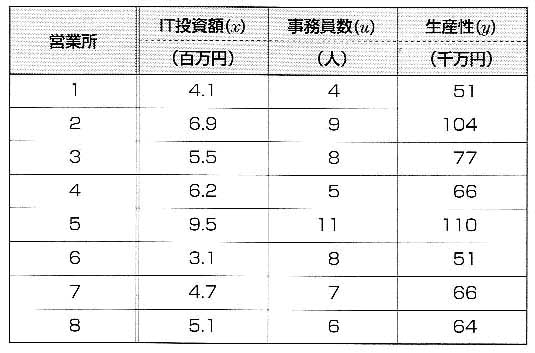
図2 ある販売会社のIT投資額データ
ここで,例えば,IT投資額の平均 は次のように求められる.
この平均![]() (=5.64)を例にして,推定と統計についてを考えてみよう.
(=5.64)を例にして,推定と統計についてを考えてみよう.
(注)標本の平均を標本平均,母集団の平均を母平均という.
まず,標本平均![]() の値5.64だが,たくさんある営業所の中からわずか8ヶ所を選んで求められた値である.
の値5.64だが,たくさんある営業所の中からわずか8ヶ所を選んで求められた値である.
この標本平均が母平均(全営業所の平均)と同じになると考える人は少ないだろう.
標本から得られる統計量が,母集団での統計量と同じになるという保証はない.
これらの標本から得られる平均や分散などの値は,標本のとり方で変わってくる.
これは統計量自体が標本の選び方によって決まる変量(すなわち確率変数)であることを示している.
つまり,平均や分散などの値は,ある規則性に従って分布しているのだ.
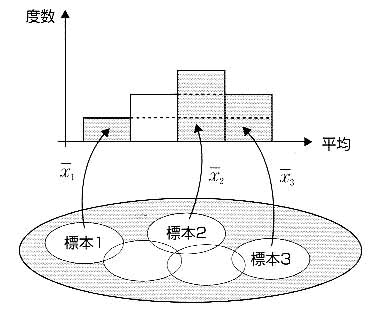
図3 いろいろな標本からそれらの平均の分布が作られる様子
それでは,いろんな標本の統計量はどのような分布になるのだろうか.統計学では,こうした分布についてよく研究されている.
ここでは,後述する推定と検定に大変重要な役割を果たす(1)正規分布(2)t分布(3)F分布をそれぞれ紹介しておく.
(1)正規分布
正規分布は次の式で表現され,図4のような分布になる.ガウス分布(関数)と呼ばれる場合もある.
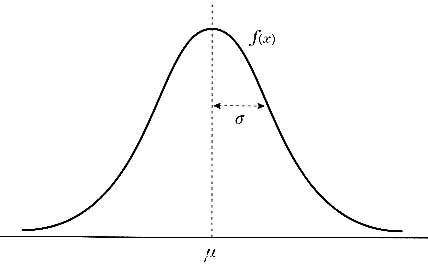
図4 平均μ,分散![]() の正規分布
の正規分布
μは平均,![]() は分散であり,数多くの標本データがあるとき,意図的に何か加工を施したものでなければ,そのデータは正規分布に従うとされている.
は分散であり,数多くの標本データがあるとき,意図的に何か加工を施したものでなければ,そのデータは正規分布に従うとされている.
有名なものとして中心極限定理というものがある.
ここに,平均がμ,標準偏差がσのある母集団があるとしよう.
その母集団から,十分大きなn個のサンプルを取り出したときの標本平均は,μのまわりに標準偏差![]() で分布するとされている(図5).
で分布するとされている(図5).
これが中心極限定理と呼ばれるものである.
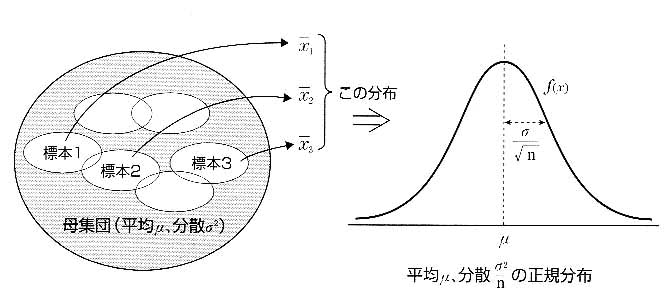
図5 中心極限定理
(2)t分布
標本数が少ない場合の標本データは,Studentのt分布(略してt分布)に従うとされている.
t分布は図6に示すような自由度pによって変化する分布であり,次の式で表される.
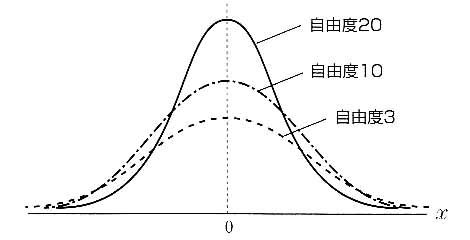
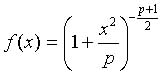
図6 t分布が描くグラフ
自由度pは,標本のデータ数nから1を引いた値n - 1で表され,自由度pを無限に大きくするとt分布は正規分布になることが証明されている.
実際は,標本数が約30個以上であれば,正規分布と考えて良いと言われている.
(1)で述べた中心極限定理では,母集団の分散(母分散)![]() が知られていることを仮定した.
が知られていることを仮定した.
しかし,実際に推定や検定を行う際には,母分散の値がわかっていることは稀である.
そこで,母分散![]() の推定値として,n個の標本から得られる不偏分散
の推定値として,n個の標本から得られる不偏分散![]() を用いる.
を用いる.
つまり,母分散![]() を
を![]() に置き換えてみる.
に置き換えてみる.
すると,次の値tは,自由度n - 1のt分布に従うことが知られている.
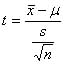
(3)F分布
F分布は自由度pとqをもち,図7のような分布になる.
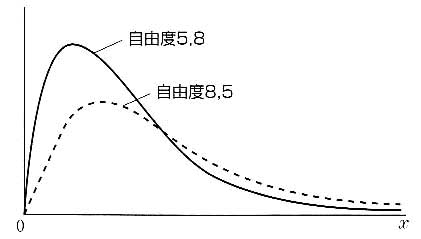
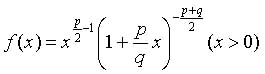
図7 F分布が描くグラフ
F分布は,標本の分散に関係する統計的な分布である.
実際,正規分布に従う母集団から各々n1,n2個の標本を選び,その分散を次のように計算する.
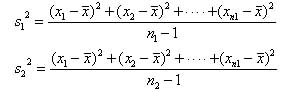
このとき,2つの分散の比![]() の分布が自由度n1- 1,n2 - 1のF分布になることが知られている.
の分布が自由度n1- 1,n2 - 1のF分布になることが知られている.
◆統計的推定の考え方
ここまでで,標本データから得られる平均や分散それ自体が確率変数(t分布など)になっていることを述べた.
このような分布が与えられると,標本データから得られる統計量から母集団についての情報を推定することができる.
具体例として,標本平均から母集団の平均(母平均)μを推定してみよう.
何度も繰り返すが,標本から得られる平均 は,それ自体が確率に従って散らばっている.
この分布(確率分布)が下図のようになったとする.
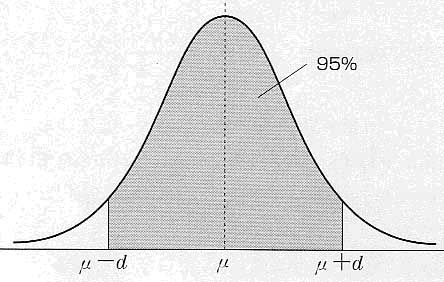
図8![]() の分布
の分布
灰色の部分は,平均μを中心に,95%の確率を覆う部分である.
標本平均 の値は,母平均μを中心に散らばることが容易に想像できる.
そして95%の確率で次の関係式が成立する.
![]() ----①
----①
この不等式を変形すると次のようになる.
![]() ----②
----②
これは,母集団の平均μが,ある標本データから得られる平均![]() から一定の幅と確率を持って区間予測されることを意味する.
から一定の幅と確率を持って区間予測されることを意味する.
②の不等式は,95%の正しさで成立する.このことを,②の信頼度は95%,あるいは,②を95%の信頼区間と表現する.
◆統計的検定の考え方
統計的検定では,ある仮説を立てその仮定が成立するか否定されるかを検証することで,検定を行う.
立てた仮説が成立することを「仮説の採択」,立てた仮説が否定されることを「仮説の棄却」という.
一般には,正規分布やt分布において95%の信頼区間内にあれば仮説が採択され,95%の信頼区間からはずれていれば,その仮説は棄却するという条件を採用している.これは,ある仮説が起こる確率が5%以下であれば,それは十分小さいとみなしているといえる.しかし,それでもその仮説を棄てたときに,まだ5%だけその仮説が正しいという可能性が残る.
つまり,5%の可能性を無視して判断したわけで,それだけ危険を冒していることになる.そこで,統計では,この5%のことを危険率と呼んでいる.あるいは,それを超えると意味がなく,それを超えなければ意味があるという意味で有意水準と呼ぶ場合もある.例えば,「5%有意水準で仮説検定する」と表現する.
さて,仮説検定の具体例をみてみよう.
例えば,日本の成人女性の平均身長は年々増加しているが,まわりの女性をみると,どうやら「日本成人女性の平均は,すでに160cmに達した」(←仮説)と思われる.これを確かめるために,日本人の20歳以上の成人女性からランダムに標本データを集めて,そのデータから,この仮説が正しいかどうかを調べたいとする.次のような10人の日本女性から標本データが得られたとしよう.

仮説である「日本人女性の平均は,すでに160cmに達した」は,つまりは母平均(日本女性すべての身長の平均)がμ=160cmというものである.
もし,標本平均が母平均を160cmと仮定したt分布の中で大きく中心からはずれた位置(通常は95%の信頼区間の外)にあるとすると,いま立てた仮説は間違いと判定されることになる(この例では,標本数が少ないのでt分布で考える).
それでは,具体的に計算を行ってみよう.
まずは,標本データの平均(標本平均)を求めると,
![]()
となり,平均身長は157.5cmということになる.
160cmに近いと思っていたが,標本の平均はそれよりも小さくなっている.しかし,まだこの時点では仮説が棄却されるとは決まっていない.
続けて,標本データの分散(不偏分散)を求めてみると,
![]()
となる.これら標本平均と不偏分散をt値の式(上のt分布の説明参照)に当てはめると,
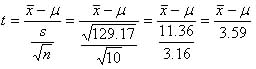
となる.ここで,仮説が採択される範囲を95%とすると,標本平均157.5cmという値が,平均を160cm(母平均)としたt分布のすその面積5%の中に入っているとき,仮説を捨てる事になる.
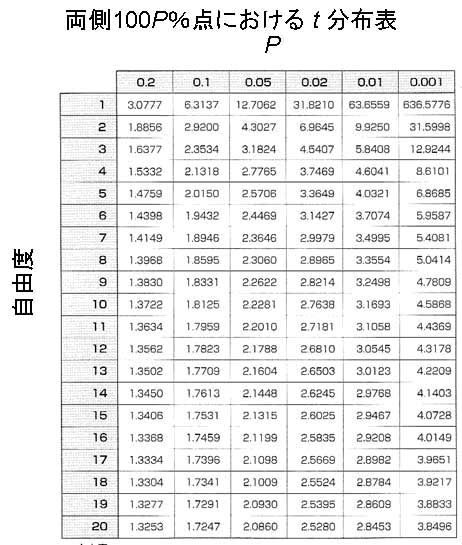
そこで,自由度が9のt分布表(下記表)から,すその面積が0.05となるt値をみると,t = 1.833となっている.
ここでは,下側のすその面積を棄却域とするので,t = -1.833となる(日本成人女性の平均身長は160cmより小さかったという過去のデータから).
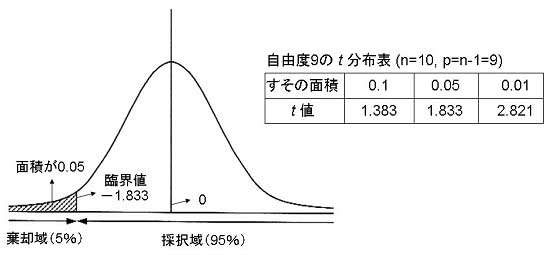
図9 採択域と棄却域
変数tは,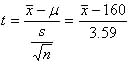 であるから,
であるから,
標本平均が母平均よりも低い方向での棄却域の臨界値は,
![]()
と与えられる.
つまり, 採択域 ![]() 棄却域
棄却域 ![]() となり,
となり,
標本の平均身長が153.4cm以下であれば「日本の成人女性の平均身長は160cmである」という仮説は棄却される.
しかし,今回の例では,標本平均が157.5cmであるので,棄却域ではない.つまりμ=160cmを否定するだけの根拠はないことになる.
ここで注意したいのは,この例での検定結果が,「日本の成人女性の平均身長は160cmである」という仮説が正しかったという結論には必ずしも結びつかない点である.ここで混乱する人がいるかもしれないが,このことについては次の帰無仮説と対立仮説で詳細を述べる.
◆帰無仮説と対立仮説
統計において仮説を立てる場合には,互いに対立するふたつの仮説を立てるのが通常である.
先の例では,
仮説1「日本の成人女性の平均身長は160cmである」
仮説2「日本の成人女性の平均身長は160cmではない」
と立てた事になる.
これらの仮説は一方が正しければ,他方は間違いであるという関係にある.
もしも仮説1を統計的に検定したときに,その起こる確率が棄却域にあれば,その仮説は棄却される.
それでは,棄却域になければどういう結論になるだろうか(先の例で実際にそうなった).
その場合は,その仮説を棄却することはできないが,かと言って,その結果から仮説1が正しいという結論をだすことはできない.
どうもあいまいで混乱する人もいるかもしれないが,実は統計の世界ではこのような仮説の立て方をする.そして,逆説的な言いまわしをすると,仮説1は棄却されてはじめて意味を持つことになる.つまり,仮説1が棄却されれば,対立する仮説2「日本の成人女性の平均身長が160cmではない」という結論を得ることができる.
言い換えれば,仮説1は無に帰してはじめて意味を持つことになる.このような仮説を,無に帰したい仮説という意味を込めて帰無仮説と呼ぶ.仮説検定においては,帰無仮説が棄却されることを半ば期待しているのである.仮説2は仮説1と対立関係にあるので,仮説1が棄却された場合に,それが正しいことが証明される.このようなある仮説と対立関係にある仮説を,対立仮説と呼ぶ.そして,結局のところ,検定の本意は対立仮説の証明にある.なお,一般的に帰無仮説はH0,対立仮説はH1と表記される.
◆両側検定と片側検定
平均身長を例に次のような二組の仮説を考えてみよう.
①仮説1「日本の成人男性の平均身長は170cmである」 H0 = 170cm
仮説2「日本の成人男性の平均身長は170cmではない」 H1≠170cm
②仮説1「イギリスの成人男性の平均身長は170cmである」 H0 = 170cm
仮説2「イギリスの成人男性の平均身長は170cmより大きい」 H1>170cm
これらの仮説を検定する場合,①の場合は170cmが平均より大きいか小さいかわからないので,信頼区間としては,分布の中心から95%の範囲を選ぶことになる.つまり,5%危険率(5%有意水準)としては,分布の両すその面積が併せて0.05(それぞれのすその面積は0,025)の値を採用することになる.
このような検定を両側検定(two-tailedtest)と呼ぶ[図10(a)].
一方,②の場合は,平均身長がはずれるとしたら170cmよりも大きい側にしかはずれることがないと予想されるので,信頼区間としては分布全体の片側の95%の範囲を選ぶことになる.つまり,5%有意水準は,片側(この場合は平均身長が170cmよりも高い側)のすその面積が0.05の値を採用することになる.
このような検定を片側検定(one-tailedtest)と呼ぶ[図10(b)].
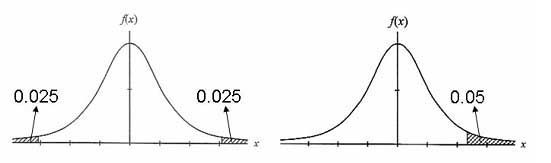
(a) 両側検定 (b) 片側検定
図10 両側検定と片側検定
さて,統計量の分布や検定について理解していただけただろうか.ここからは本題のROCの統計的有意差検定の話に戻る.
ROC解析では,2つの画像システムの検出能の差を評価する場合,「2つのシステム間では差がある」という仮説を証明するために,「2つのシステム間では差がない」という帰無仮説を立てる.つまり,「2つのシステム間では差がない」という仮説の棄却を期待し,「2つのシステム間では差がある」という結果を得たいのである.
2本のROC曲線の有意差検定を行う場合を考えて見よう.ROC曲線の検定では「Az」を検定に利用する.つまり,2つのシステムのROC曲線の下側の面積Az値が同一である場合,2つのシステムは同一と考える.そして,ROC解析での検定法としては,t検定やJackknife法がよく知られている.
t検定の方法は,先述の「統計的検定の考え方」で述べた通りであり,t分布を利用して検定が行われる.Jackknife法では,F分布を用いてF検定を行うがその計算過程は非常に複雑である.そのため,ここでは,t検定によるROC曲線間の有意差検定について述べるに留める.それでは,具体的に2本のROC曲線間でt検定を行う手順を例を通して見てみよう.
★例1
6人の観察者が,増感紙ーフィルム系で撮影された胸部X線単純写真とその写真をデジタル化し2/3に縮小した後レーザープリンターで出力した画像を用いて,悪性腫瘤陰影の検出率についてROC解析を行った.
観察者は全員経験5年以上の放射線医で,資料枚数はpositive像50枚,negative像40枚を用いた.その結果として各観察者ごとに得られたROC曲線のAz値が次の表のようになった.Az値を指標に用いて,オリジナル画像と2/3縮小されたディジタル画像間で悪性腫瘤陰影の検出率について差がみられるかどうかをt検定で5%有意水準で仮説検定してみよう.
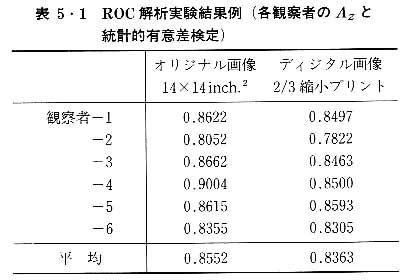
はじめに帰無仮説と対立仮説を立てる.
帰無仮説H0 「オリジナル画像と2/3縮小されたディジタル画像間の悪性腫瘤陰影の検出率には差がない」 (=両画像での検出率は同じ)
対立仮説H1 「オリジナル画像と2/3縮小されたディジタル画像間の悪性腫瘤陰影の検出率には差がある」 (=両画像での検出率は異なる)
計算手順は次の通りである.
① 観察者ごとに両画像で得たAz値の差をとる.→標本データ
② 標本データの標本平均![]() と不偏分散
と不偏分散![]() を求める.
を求める.
③ t分布表から自由度n - 1の棄却域(5%)のt値を読み取る.
④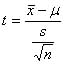 に μ,s ,t を代入し,棄却域の臨界値を求める.
に μ,s ,t を代入し,棄却域の臨界値を求める.
⑤ 棄却域を 【 ![]() ④で求めた値×(-1) or
④で求めた値×(-1) or ![]() ④で求めた値】(両側検定) とし,標本平均
④で求めた値】(両側検定) とし,標本平均![]() が棄却域にあるか調べる.
が棄却域にあるか調べる.
手順に従って計算すると....
①

② ![]() = 0.018833,
= 0.018833,![]() = 0.000304619
= 0.000304619
③ 標本数はn=6なので,t分布表から自由度5,P=0.05のt値を読み取ると,t = 2.5706が得られる.
④ ![]() よって,
よって, ![]() となる.
となる.
(2つの画像間で検出率に差がないと仮定したときμ= 0となる)
⑤棄却域は, ![]() -0.018316 or
-0.018316 or ![]() 0.018316となり,
0.018316となり,![]() = 0.018833は棄却域にあるので,「オリジナル画像と2/3縮小されたディジタル画像間の悪性腫瘤陰影の検出率には差がない」という仮説は棄却される.よって,対立仮説が成立し,オリジナル画像と2/3縮小されたディジタル画像での悪性腫瘤陰影の検出率は同じではなく「差がある」という結論が得られる.
= 0.018833は棄却域にあるので,「オリジナル画像と2/3縮小されたディジタル画像間の悪性腫瘤陰影の検出率には差がない」という仮説は棄却される.よって,対立仮説が成立し,オリジナル画像と2/3縮小されたディジタル画像での悪性腫瘤陰影の検出率は同じではなく「差がある」という結論が得られる.
|
実験1: ROCTESTで描いた難易度別のROC曲線の面積Az値を利用して,5%有意水準でt検定による仮説検定を行いなさい.(n≧10程度のデータを用いる) |
|
方法:
|