図1 刺激-反応マトリックス
【概要】
ROC解析(Receiver Operating Characteristic analysis)は,第2次世界大戦中に飛行機を発見するレーダー・システムの性能評価を目的として考案された方法である.飛来する物体が飛行機なのか鳥の群なのか,低空飛行をしている飛行機が認識できるかどうかといったレーダー・システムの能力を評価するために開発された.その後,人間の視知覚検出の性能を評価するために応用されるようになり,さらに放射線画像診断の判断意思決定の評価に適用されるようになった.
これは,「レーダー・システム」を「放射線画像システム」に,「飛来する飛行機」を「病変」に,「鳥の群」を「人体の正常構造」に置き換えて考えればよい.
つまり,画像診断における”診断の正確さ”を評価するために応用されたわけである.さらに,近年のコンピュータ支援診断(Computer Aided Diagnosis : CAD)の開発に伴い,CADシステムの性能評価にもROC解析が利用されるようになった.この他にもROC解析は医用画像情報を扱う分野において様々な方面で応用されており,今もなお進歩の過渡にある非常に重要な評価方法のひとつである.画像評価の方法は,”物理評価”と”視覚評価”に大きく分けることができる.医用画像における物理評価法の代表例としては,コントラストを示す特性曲線,鮮鋭度を評価するMTF,粒状性を評価するウィナースペクトル,総合評価としてのNEQやDQE,などを挙げることができる.
一方,視覚評価法としては,ROC解析,一対比較法,CDダイヤフラム法(バーガー・ファントム法),ハウレット・チャート法,ランドル環法といったものが挙げられる.これらの中で,実際の病変を含む画像を対象として診断能を求めることができる評価法は,ROC解析と一対比較法が適当と考えられており,さらに,統計的な手法の検討が十分に行なわれているROC解析は,最も信頼性の高い評価法であるとされている.なお,画像評価における物理評価は”客観的な評価”であり,視覚評価は”主観的な評価”であると言える.客観的な評価は,物理的な特性を測定することに相当し,主観的な評価は,観察者の主観に基づいて真実を推定することに相当する.ROC解析は主観的な評価である.
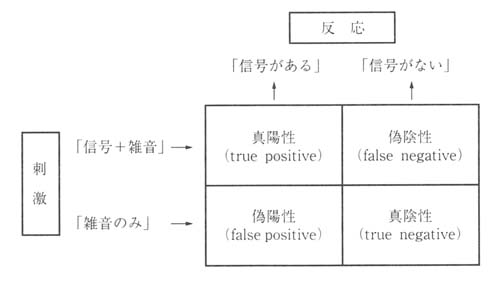
ROC解析は,信号処理の観点では「雑音」のなかに埋もれている「信号」を検出する能力や性能を評価する方法である.信号検出理論では,観察者への入力(刺激)とその出力(反応)が図1のような刺激-反応マトリックスで示される.なお,これを医用画像での視覚評価の観点から見ると,「雑音」は「人体の正常構造」に,「信号」は「病変部の陰影」に相当することになる.

図1 刺激-反応マトリックス
ある観察者に雑音のみの画像(ネガティブ像)と雑音に信号が含まれている画像(ポジティブ像)の2種類を提示し,「その中に信号はありますか?」と質問した場合
観察者の回答は,「信号がある」か「信号がない」のどちらかにしかならない.つまり,出力(反応)は次の4種類に分類される.
(1)真陽性(true positive:TP) ポジティブ像を観察して,正しく「信号がある」と答える.
(2)偽陰性(false negative:FN) ポジティブ像を観察して,誤って「信号がない」と答える.
(3)偽陽性(false positive:FP) ネガティブ像を観察して,誤って「信号がある」と答える.
(4)真陰性(true negative:TN) ネガティブ像を観察して,正しく「信号」がないと答える.
この場合の「信号がある」か「信号がない」かの判断を決定する基準を観察者の判断基準と呼ぶ.
判断基準が変化することによって,4つの反応の確率も変化する.
ただし,真陽性=(1-偽陰性),偽陽性=(1-真陰性)の関係にあることを副えておく.
ここで,判断基準によって4つの反応の確率が変化するという事実を,天気予報の的中率を例に考えてみよう.
表1は,例えば,とある1週間の新潟市内の天気予報とその日に実際に観測された気象情報であるとする.
また,その1週間に,A太君,B子さん,C子さんの3名に毎日「今日の天気予報は当たりましたか?」という質問をし,その答えをまとめたものが表2であるとする.

表1 とある1週間の新潟市内の天気予報と実際に観測された気象情報

表2 A太君,B子さん,C子さんからみた天気予報の的中率
○:天気予報は当たった,×:天気予報ははずれた
さて,表1で実際に観測された気象情報が正しいとすると,A太君,B子さん,C子さんのそれぞれの判断基準に基づいてTPとFPを算出すると,表3のようになる.ただし,天気予報が当たった日をポジティブデータ,天気予報がはずれた日をネガティブデータとする.
表3は,天気予報と実際の天気の様子を3名ともに同じ入力(刺激)として与えたにも関わらず,それに対する出力(反応)は個人によって異なっていることを示している.これは「天気予報は当たりましたか?」という質問に対する各個人の判断基準が異っているからである.
また,この例では個人間の判断基準の違いを挙げたが,同一人物であっても判断基準が異なってくる場合もある.
つまり,毎日「今日の天気予報は当たりましたか?」という質問に答えてもらうのと,週末にまとめて「今週の各曜日の天気予報は当たりましたか?」という質問に答えてもらうのでは,例え同一人物が判断を下すにしてもその反応は異なってくる可能性がある.
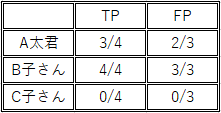
表3 A太君,B子さん,C子さんの反応結果(TP率,FP率)
医用画像を診断する際にも,判断基準の変化や違いが伴うことは想像できるであろう.
このことに基づいて,ROC解析では,観察者がネガティブ像,あるいはポジティブ像を観察したときの判断基準の変化や違いに伴う反応が,それぞれ独立した「正規分布になる」と仮定している.このような仮定に基づいたROC解析法を特に連続確信度法と呼ぶ.*)
さて,この仮定に従うと図2のような両正規分布が得られる.
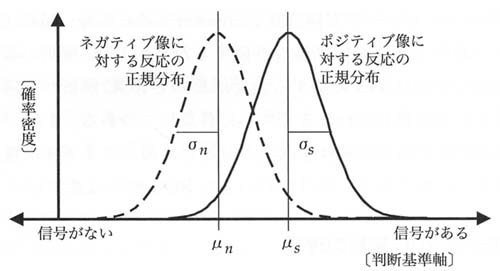
図2 ネガティブ像とポジティブ像に対する観察者の反応の正規分布
ROC解析では通常,図1の反応マトリックスにおけるFPとTPを評価に用いる.
このことからネガティブ像における判断基準値の正規分布関数をFP(x),ポジティブ像の正規分布関数をTP(x)とすると,それらは以下の式で表される.
μn,μsはそれぞれ分布の平均値であり,σn,σsはその標準偏差である.
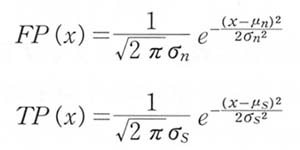
ROC曲線はFP(x),TP(x)から算出することができる.
ROC曲線の縦軸はTPF:true positive fraction,横軸はFPF:false positive fractionで表わされる.
TPF,TFPはそれぞれ+∞から任意の判断基準値xまでのTP(x)およびFP(x)の部分積分を,TP(x)およびFP(x)の全積分で正規化したものである.
図3をみてみよう.
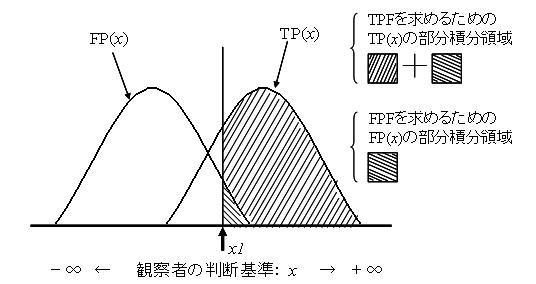
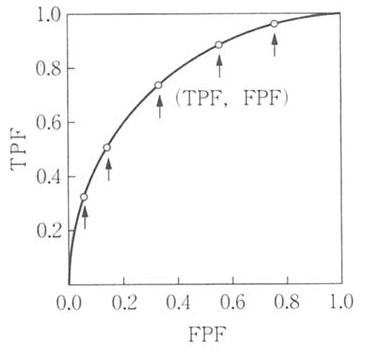
図3 両正規分布と観察者の判断基準,およびROC曲線の関係
図3は判断基準を5つ設定したときの例である.判断基準xは" ↑ "で示されている.
中央の" ↑ "を例にとると,TPFは斜線部+灰色部分の面積をTP(x)全体の面積で割った値となる.
同様にFPFは,灰色部分の面積をFP(x)全体の面積で割った値となる.このようにTPFとFPFは,0~1.0間の実数で求められる.
判断基準を連続的に変化させると図3の右グラフのような曲線を描くことができる.これがROC曲線と呼ばれるものである.
ROC曲線は左上角に近づくほど,信号の検出能が高いことを示し,逆に正の対角線に近づくほど信号の検出能が低いことを示す.
*) ROC解析によく用いられる方法として,評定確信度法と連続確信度法がある.
評定確信度法では,観察者は各観察資料を判断基準ごとのカテゴリー(通常は5段階,「信号は絶対ある」,「信号はたぶんある」,「わからない」,「信号はたぶんない」,「信号は絶対にない」)に分類する.この手法は古典的な手法であり現在もよく用いられている方法ではあるが,観察者間の変動が大きくなるという問題点を持っている.一方,連続確信度法では,観察者は各観察資料に対して,判断基準に応じた自由な尺度でスコアをつけ(例えば,「信号がある」という確信度を0~100%で示す),理論的にカテゴリ分類を行うことでROC曲線を描く.
このことにより,観察者間の変動は少なくなり,さらに反応に用いられる値に尺度の制約がないので,観察実験以外の評価(例えば,コンピュータ支援診断システムの性能評価など)にも適用することができる.ただし,実験結果から正規分布を推定するには複雑な計算を要する.
このようなROC解析を用いることで,観察者(読影者)間の信号検出(読影)能力を比較することができる.
例えば,同じ画像を複数の読影者が観察することで,読影者ごとのROC曲線が描ける.また,モダリティ別の診断能を比較することができる.
例えば,同じ部位を撮影したCT画像とMR画像を用いれば,CT画像での診断能を表すROC曲線とMRI画像での診断能を表すROC曲線がそれぞれ描ける.
このように複数のROC曲線を比較する場合は,統計的有意差検定を行う必要がある.
一般にROC曲線間の統計的有意差検定には,各観察者のAz値(ROC曲線下の面積)を用いる両側t検定と,各観察者のすべてのスコアを用いて二次元分散分析を行うJackknife法が用いられる.ただし,Jackknife法は連続確信度法にのみ適用できる手法である.
観察実験で得られた各観察資料の得点(観察者の判断基準に応じてつけられた得点)を元に,両正規分布を推定し,そこからROC曲線を算出する一連の計算手順をカーブフィッティングと呼ぶ.このカーブフィッティングの過程において,両正規分布の平均値と分散を推定する作業は特に複雑な計算を要する.
このような計算をすべて行ってくれるソフトウェアにROCKITがある.ROCKITは,シカゴ大学のMetzらによって開発されたROC解析ソフトであり,パソコン用として一般に公開され,インターネット経由(シカゴ大学のホームページ上)で無償で入手することができる.
さて,以下はROC曲線を手計算で求める方法である.この計算方法は簡便で汎用性が高いが,正規性の検定が行われていない.
1.各試料につけられた得点を,ポジティブ,ネガティブの画像に関係なしに大きいものから順に配列する.
2.それらの配列を,適当に等分し(5等分,10等分など),大きいものからカテゴリ番号をつける.
3.各カテゴリに含まれるポジティブ像,ネガティブ像の数をそれぞれ求める.
4.i番目のカテゴリまでに含まれるポジティブ像の数をΣP(i),同様にi番目のカテゴリまでに含まれるネガティブ像の数をΣN(i)とし,次の式を当てはめ,ROC曲線の各点の座標(TPF(i),FPF(i))を求める.
TPF(i) = ΣP(i)/P (P:ポジティブ像の総数)
FPF(i) = ΣN(i)/N (N:ネガティブ像の総数)
5.4で求まった各点をプロットし,ROC曲線を描く.
*)評定確信度法では,はじめから5段階にカテゴリ分類されているために,手順3からはじめる.
|
実験1: 手計算でROC曲線を描いてみよう! |
|
方法:

|
|
実験2: 胸部X線画像データベースを試料としたROC解析実験を行ってみよう! |
|
方法:
|