7.2値画像処理
【概要】
2値画像とは白と黒の2つの値のみで表される画像である.
2値画像処理は,画像中の対象の輪郭や領域などを決定するときによく用いられる処理である.
濃淡画像において,ある値を境にして白と黒の2つの画素値(2値)で表す処理を一般的にしきい値処理と言う.
そして,境の値を”しきい値’と呼ぶ.また,しきい値処理とよく似た処理に域値処理というのがあるが,これは,ある濃淡値の範囲のみを表示する処理である.
|
|
使用する画像:
演習1-1で使用した胸部X線画像
方法:
1.Image-Jを起動後, 対象画像を開く.
⇒「File」→「Open」を押し, 対象画像を選択.
2.2値画像を作成する.
⇒「Process」→「Binary」→「Make Binary」を選択.
自動的に適当なしきい値が設定され2値画像が作成される.
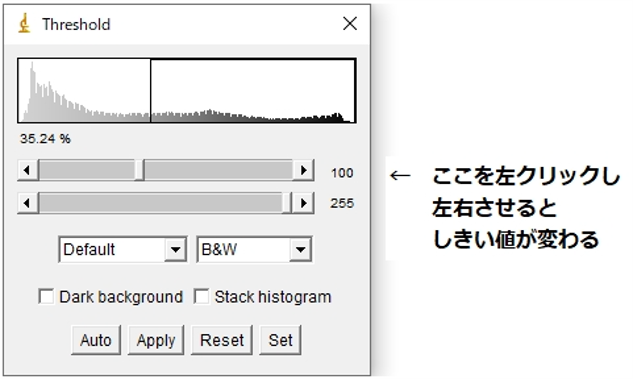
3.しきい値を変更する.
「Image」→「Adjust」→「Threshold」を選択. LUTウィンドウでしきい値を変更することができる.
考察:
・しきい値処理と域値処理の違いをまとめてみよう.
|
|
|
使用する画像:
演習1-1で使用した胸部X線画像
方法:
1.Image-Jを起動後, 対象画像を開く.
⇒「File」→「Open」を押し, 対象画像を選択.
2.しきい値を変更する.
⇒「Image」→「Adjust」→「Threshold」を選択.
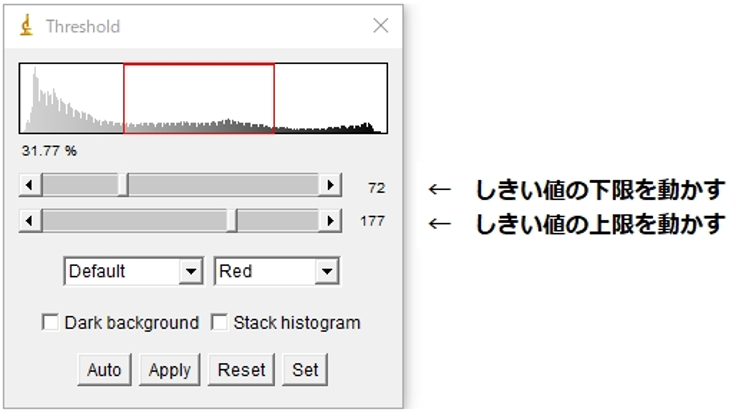
* 「Threshold」の ”B&W”を”Red”に変更, LUTウィンドウでしきい値を変更することができる.
3.域値を変更する.
LUTウィンドウで域値の上限, 下限, 範囲を変更することができる.
考察:
・肺野内部の領域のみを表示する域値範囲を探してみよう.また,肺野内以外の脂肪領域を表示する域値範囲を探してみよう.
|
【モルフォロジ処理】
モルフォロジ処理は,”構造要素”と呼ばれる画像を移動させる要素と,”ミンコフスキー(Minkowski)和・ミンコフスキー差”と呼ばれる演算から成り立っている.
モルフォロジ処理における代表的な処理は,「Erosion(エロージョン)」と「Dilation(ダイレーション)」と呼ばれる処理であり,それぞれ孤立点の除去,不連続な点の接続と穴埋めのために利用される.
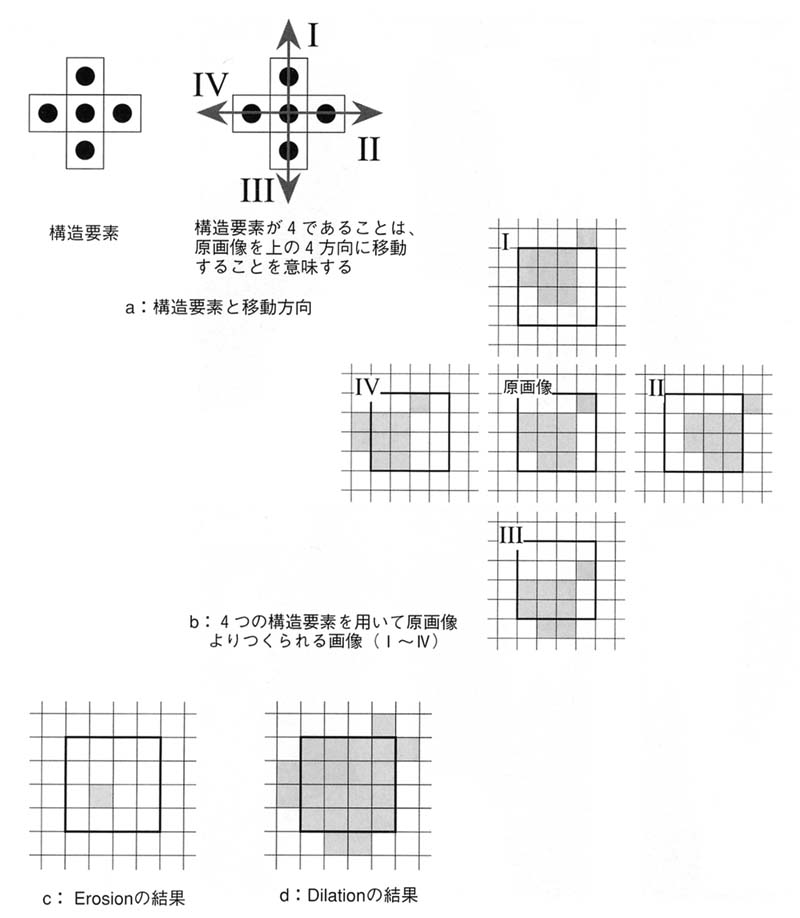
図1 モルフォロジ処理の原理
図1はモルフォロジ処理の原理を示している.aは構造要素の一例である.
これは,原画像のパターンを上下左右の4方向にずらしたパターンを作成することを意味する.
bはある原画像パターンを構造要素aでずらしたパターン例である.
「Erosion」と「Dilation」は,これら4つのパターンのミンコフスキー差(論理積)とミンコフスキー和(論理和)を計算することで実現できる.
つまり,ミンコフスキー差はすべての構造要素からつくられたパターンの共通領域のみを計算結果として出力し,ミンコフスキー和は存在領域をすべて計算結果として出力する.
cは「Erosion」の結果,dは「Dilation」の結果である.これらは,膨張,収縮のための処理として利用することができる.
また,モルフォロジ処理には,「Opening」と「Closing」という処理がある.
「Opening」は「Erosion」の後に「Dilation」,「Closing」は「Dilation」の後に「Erosion」を行う処理である.
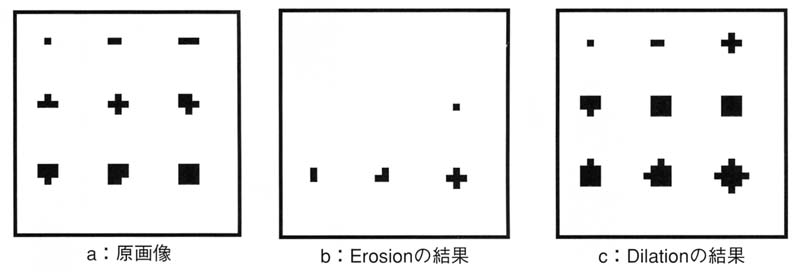
図2 ErosionとDilationの結果例
図2は9つのパターンに対して,ImageJで「Erosion」と「Delation」を行った結果の一例である.
結果をよく観察すると「Erosion」と「Dilation」の結果が,図1で示したモルフォロジの原理通りに実行されていないことに気づく.
これは,ImageJではモルフォロジ処理が忠実に行われず,ほぼ等価な条件判断で実現されているため,純粋なモルフォロジ処理とは異なる結果になるからである.
ImageJでは,いわゆる画像における膨張,収縮処理と呼ばれるものになる.
「Erosion」は黒い画素の収縮処理に当たり,ある注目する黒い画素を中心としてその8近傍を見たとき,その8近傍に白い画素が一定数以上存在する場合のみ注目する黒い画素を削除することで実現する.
「Dilation」は,黒い画素の周辺のある白い画素を中心としてその8近傍を見たとき,その8近傍に黒い画素が一定数以上存在する場合のみ注目する白い画素を黒い画素に置き換えることで実現する.
なお,ImageJでは,「Erosion」は「Erode」,「Dilation」は「Dilate」と表示されている.
演習7-3:2値画像でのモルフォロジ処理を実践してみよう!
|
使用する画像:
図2で示した画素パターン(2値画像, tiff形式)
方法:
1.Image-Jを起動後, 対象画像を開く.
⇒「File」→「Open」を押し, 対象画像を選択.
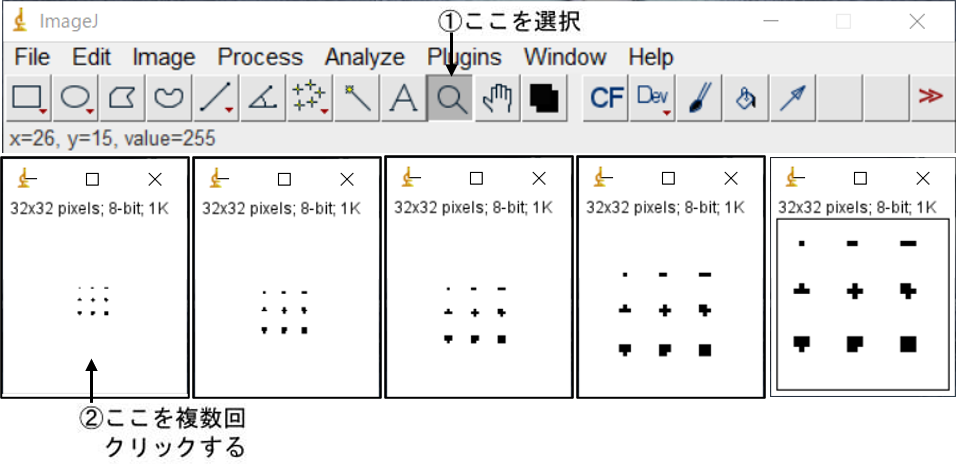
*)原画像を大きく表示したい場合は,拡大ツールを使用する.
2.収縮処理と膨張処理を実行する.
⇒収縮処理:「Process」→「Binary」→「Options」の”Count”および”Iterations”を適宜変更, ”Do”→「Erode」を選択.
⇒膨張処理:「Process」→「Binary」→「Options」の”Count”および”Iterations”を適宜変更, ”Do”→「Dilate」を選択.
*)「Process」→「Binary」→「Iterations(1-100)」でStep2の処理を反復することができる.
*)「Process」→「Binary」→「Count(1-8)」でカウントする近傍の画素数を設定することができる.
考察:
・膨張処理,収縮処理を実行し,図2のb,cと同一の結果が得られるかどうか確認してみよう.
・「Options」の設定値をいろいろ変えることによって,また,同じ処理を何回も繰り返す(同じ条件下で膨張 or 収縮処理を複数回繰り返す,など)ことによって,結果がどのように変化するか確かめてみよう.
・図1の構造要素を使って純粋なモルフォロジ処理を行ったときのパターンを作画し,この演習での結果と比較してみよう.
|
演習7-4:モルフォロジ処理を使って目的とするパターンを作ってみよう!
|
使用する画像:
下に示す初期パターン(2値画像,tiff形式)

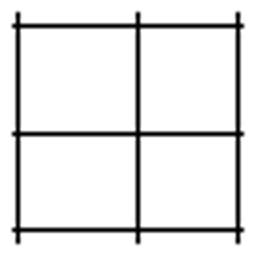 初期パターン 目的パターン
方法:
1.Image-Jを起動後, 対象画像を開く.
⇒「File」→「Open」を押し, 対象画像を選択.
*)原画像を大きく表示したい場合は,拡大ツールを使用する.
2.収縮処理と膨張処理を実行する.
⇒収縮処理:「Process」→「Binary」→「Options」の”Count”および”Iterations”を適宜変更, ”Do”→「Erode」を選択.
⇒膨張処理:「Process」→「Binary」→「Options」の”Count”および”Iterations”を適宜変更, ”Do”→「Dilate」を選択.
*)「Process」→「Binary」→「Iterations(1-100)」でStep2の処理を反復することができる.
*)「Process」→「Binary」→「Count(1-8)」でカウントする近傍の画素数を設定することができる.
考察:
なぜその手順でうまくいったのか整理しながら,目的パターンにいたるまでの手順をまとめてみよう.
|
実験項目へ戻る