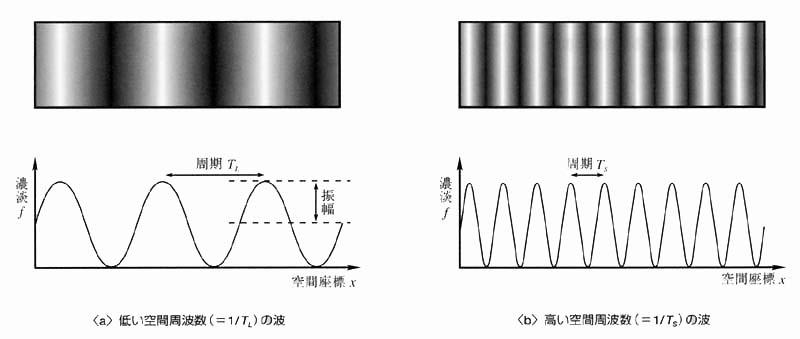
図1 空間周波数の例
【フーリエ変換の概要】
フーリエ変換の概念を理解する上で,重要なキーワードに”空間領域”と”空間周波数領域”がある.
フーリエ変換とは,この2つの領域の片方からもう片方へ信号を変換する数学的な操作である.
空間領域とは,距離の空間とも説明することができる.これまでの演習で扱ってきた通常のX線画像や処理は,空間領域のものである.
それに対して,空間周波数領域とは,信号がどのような周波数成分を持っているのかを表す空間であると説明できる.
電波や音波に関して使われる周波数は,単位時間(1秒間)に通過する波の数を意味し,波の周期をTとするとその逆数1/Tで与えられる.
それに対して空間周波数領域は,単位長さ(たとえば1mm)中に存在する明暗の縞模様で表される波の数を意味し,同様に波の周期の逆数で定義される.
電波や音波の周波数が時間軸上で定義されるのに対して,空間周波数は空間軸上で定義される点が異なる.図1を見てみよう.

図1 空間周波数の例
{a}は濃淡がなだらかに変化するパターンであり,低い空間周波数を持つ.
{b}は{a}より濃淡が激しく変化するパターンであり,{a}に比べ高い空間周波数を持つ.
任意の周期波形は,振幅,周波数,位相(波の進行方向のずれ)が異なる数多くの正弦波を重ね合わせる(和をとる)ことによって表すことができる.
図2は4つの異なる正弦波を合成すると得られる結果が徐々に矩形波に近づいていく様子を示したものである.
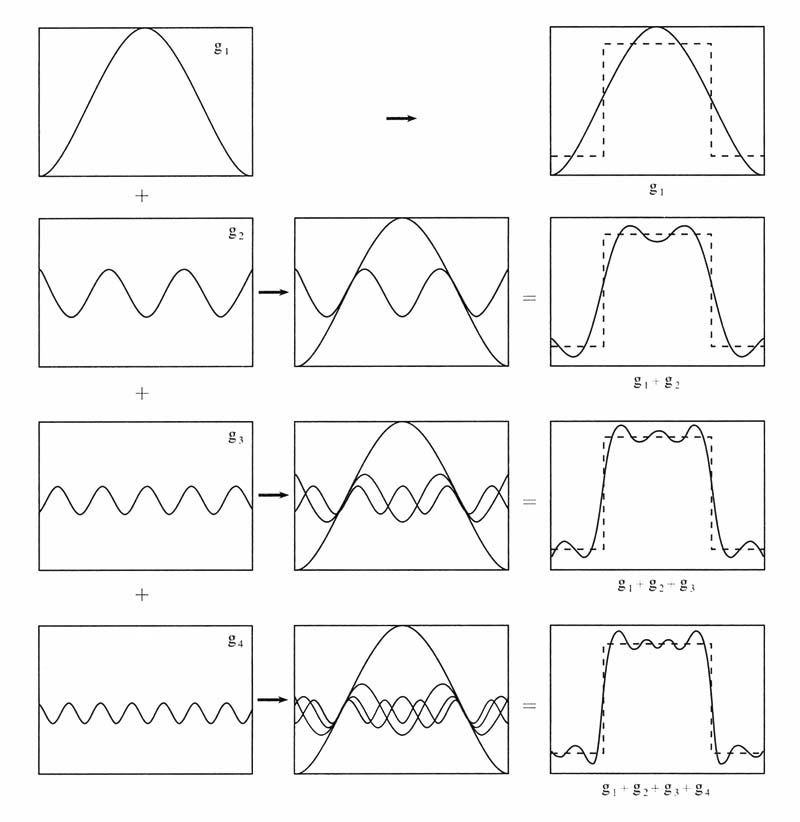
図2 正弦波の合成による矩形波の表現
図2の4つの波の振幅を縦軸に,周波数を横軸にとったグラフを示すと図3の実線のようになる.
また,4つよりもさらに多くの正弦波を合成すれば,得られる結果はより矩形波に近づくが,それらの正弦波の振幅と周波数も図3に示してある.
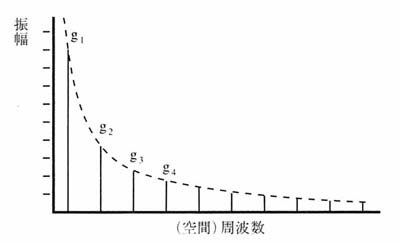
図3 矩形波の周波数成分(振幅スペクトル)
図2,図3から,矩形波は図3で示した振幅と周波数を持つ複数の正弦波から構成されていると考えることができる.
矩形波を構成する各周波数の正弦波は,元の矩形波を構成する周波数成分としての意味を持ち,それらを周波数スペクトルという.
周波数が空間周波数である場合は,空間周波数成分を意味し,空間周波数スペクトルという.
また,図3では縦軸を振幅に対応させたが,その場合を特に振幅スペクトル,位相を縦軸に対応させた場合を位相スペクトルという.
図2および図3の例は,数学的にはフーリエ級数による矩形波の分解・合成を示したものである.
矩形波のような波形であっても,振幅と位相および周波数が異なる数多くの正弦波に分解され,また分解された正弦波から元の矩形波を合成できるという原理を概念的に理解できるであろう.
この原理の基礎になっているのは,「任意の波形は,単純な正弦波の和で表現できる」ことにあり,この処理を実践しているのがまさにフーリエ変換である.
つまり,フーリエ変換は,ある波形を異なる振幅や周波数,位相をもつ数多くの正弦波に分解する.
逆に,フーリエ逆変換は,分解された数多くの正弦波を重ね合わせて元の波形を再生する.(図4)
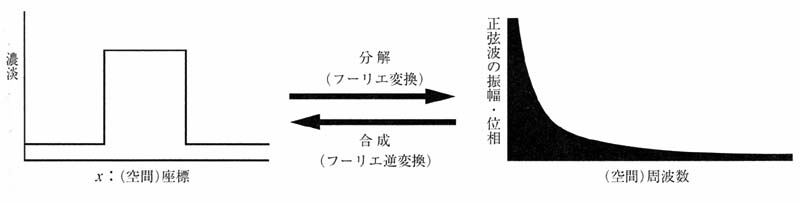
図4 ある波形の正弦波への分解と正弦波からの合成
【画像のフーリエ変換】
これまで述べてきたフーリエ変換は2次元信号である画像にも適用することができる.
ただし,通常,フーリエ変換で扱おうとする画像は,標本化されたディジタル信号であり,また,数学上では無限大という考えが通用するが(フーリエ変換の式では∞が使用されている),コンピュータでは有限回の計算で終わらなければならない.
このような制約をうけたフーリエ変換を特に「離散的フーリエ変換」(DFT:Discrete Fourier Transform)と呼んでいる.
詳細は省くが,DFTは三角関数と積和計算だけで表されており,コンピュータで計算させることが可能となる.
しかし,DFTにも計算量が膨大になるという問題がある.
そこで考案されたのが,「高速フーリエ変換」(FFT:Fast Fourier Transform)というアルゴリズムであり,データ数が2のべき乗個の場合のみに限定されるが,計算量を大幅に減らすことができる.
そのため,ディジタル画像のフーリエ変換処理にはほとんどの場合FFTが用いられる.
画像を周波数で考えたとき,2次元信号であることから,水平方向と垂直方向の二つの周波数を持つことは容易に想像することができる.
通常,画像にFFT処理を行うときは,図5に示すように,1次元FFTを横方向に行い,その次にもう一度1次元FFTを縦方向に行うことで実現している.
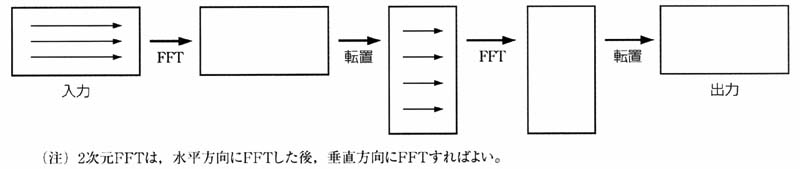
図5 画像(2次元)へのFFTの手順
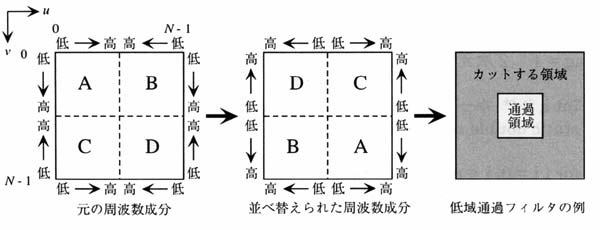
水平周波数を u ,垂直周波数を v として,図5の手順でFFTを行うと,図6(a)のような空間周波数スペクトルを得ることができる.
通常,画像においては,(a)をA,B,C,Dに分割し,(b)のように再統合することで,中心付近が低周波成分そして中心から離れるに従って高周波成分になるスペクトルを利用することが一般的である.
これは周波数領域でのフィルタ処理を行う際に便利であるからである.
例えば,(c)は低域通過フィルタであり,このフィルタを通過させた後の画像では,高周波成分がカットされることになる.
なお,濃淡変化が緩やかな画像(たとえばぴんとがずれてぼけた画像)は,高い空間周波数成分が小さくなる.
細かい模様の多い画像やエッジのように急激に濃淡が変化するようなパターンを含む画像(たとえば鮮鋭な画像)は,高い空間周波数成分が大きくなる.
参考までにフーリエ変換後の空間周波数と実際の画像との関係を図7に示す.
(a) (b) (c)
図6 2次元空間周波数スペクトルと低域通過フィルタの例
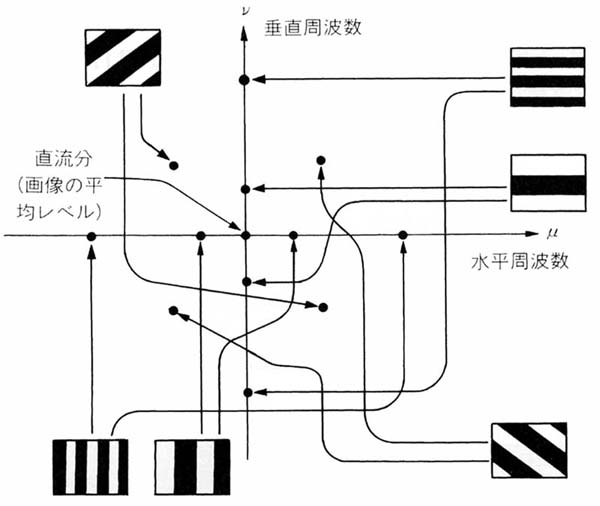
図7 2次元空間周波数スペクトルと画像の関係(図6(b)に対応する)
|
演習5-1:横方向の縞模様画像にフーリエ変換処理を実践してみよう! |
|
方法:
考察:
|
|
演習5-2:低周波遮断フィルタと高周波遮断フィルタを実践してみよう! |
|
方法:
考察:
|
|
演習5-3:胸部X線画像にフーリエ変換処理を施してみよう! |