
図1 一次元におけるたたみ込みの演算の計算例
【たたみ込み演算】
たたみ込みは,画像処理を実行するときに最も頻繁に用いられる計算のひとつである.
数学的には,もとの関数とたたみ込む関数との積分で表されるが,ディジタル信号においては,掛け算と足し算のみで容易に表現することができる.
図1を見てみよう.これは一次元信号に対するたたみ込みの演算例である.

図1 一次元におけるたたみ込みの演算の計算例
この例では,関数 f に関数 g をたたみ込み,その結果を f *g として表している.
b',c' と進むにつれて,関数 g が1つずつずれて掛け算が行われていることがわかる.
ただし,関数 f において両端の a と g については,関数 g をずらしていった際にそれぞれの x と z とが関数 f の範囲から外れてしまう.
そのため,計算結果の a' と g' は,強制的に出力画素値を0とするか,または適切な処理方法を定義して計算を行う必要がある.
このたたみ込みを二次元に拡張すれば,そのまま画像に適用することができる.図2を見てみよう.
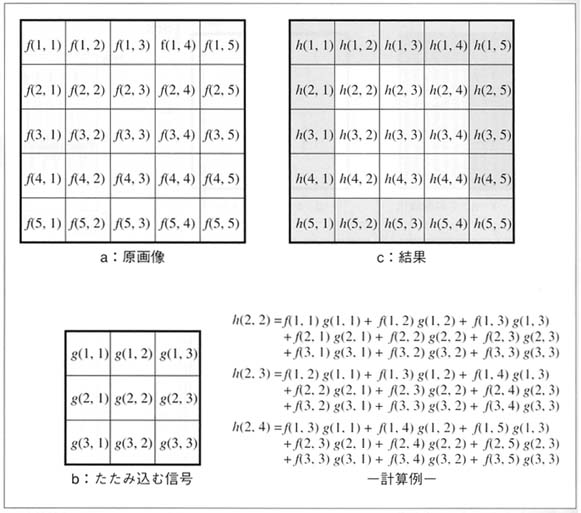
図2 画像におけるたたみ込みの演算の計算例
原画像 a に信号 b をたたみ込んだ結果がcである.
計算例に示す通り,一次元信号における計算を単純に二次元に拡張しただけである.
計算量は増えているが,掛け算と足し算のみで実行されていることに変わりはない.
また,c において灰色で示されている端の画素値は,適切な処理方法を定義して計算を行う必要がある.
|
演習4-1:たたみ込み演算を手計算で行ってみよう! |
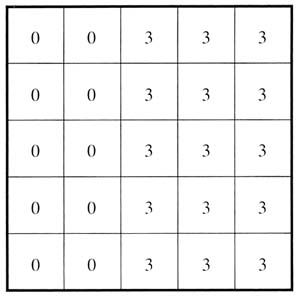 
a.原画像 b.たたみ込む信号 方法:
考察:
|
【平滑化】
平滑化(スムージング,smoothing)は,画像上の濃淡変動を滑らかにする処理のことである.
雑音の低減を図る場合や画像をぼかす効果を得たいときに使用される.
平滑化の方法は,2種類に大別される.
すべての濃淡変動を一様に平滑化する方法としては,移動平均フィルタリング,加重平均フィルタリングなどがある.
エッジや線など大きな濃淡変化を保存しながら微小な変動のみを選択的に平滑化する方法としては,可変加重平均フィルタリング,k最近隣平均フィルタリング,メディアンフィルタリングなどがある.
・移動平均フィルタリング: 注目画素を中心とする局所領域の平均値をその注目画素に出力するフィルタを,対象画像のすべての画素に適用する方法である.
局所領域のすべての画素に対して同じ重み係数が使用される.演習4-1のbは,移動平均フィルタの一例である.
・加重平均フィルタリング: 注目する中心画素に対して周辺の画素の寄与は小さいと仮定したフィルタ処理.
平滑化の程度を重み係数を変えることによって制御できる.移動平均フィルタと比べ,より緩やかな平滑化を行うことができる.
現実の撮影系に存在するボケのカーネル分布は,ガウス分布をもつことが知られており,そのため正規分布型の重み係数が使用されることが多い.
このようなフィルタを特にガウシアンフィルタ(Gaussian Filter)と呼ぶ.
・メディアンフィルタリング: 局所領域における濃淡のレベルの中央値(Median)を出力するフィルタである.
エッジ情報が保存されやすい特徴を持っている.特にスパイク状の雑音(ごま塩雑音とも呼ばれる)を容易に取り除くことが可能である.
|
演習4-2:たたみ込みによる画像の平滑化を体験してみよう! |
|
使用する画像:
胸部X線画像
方法:
考察:
|
【雑音の除去】
一般に,雑音の濃度と,その周りの濃度には急激な濃度差がある.
逆に,急激な濃度差があるから目障り(雑音)なわけである.
このような雑音は,平滑化を利用して除去することができる.
ただし,目的画像のエッジの部分も急激な濃度差があるので,このエッジ部分と雑音部分をいかにして分離して雑音だけを除去するかが,平滑化処理では重要になる.
胸部X線画像に故意に雑音を乗せた画像を図3に示す.
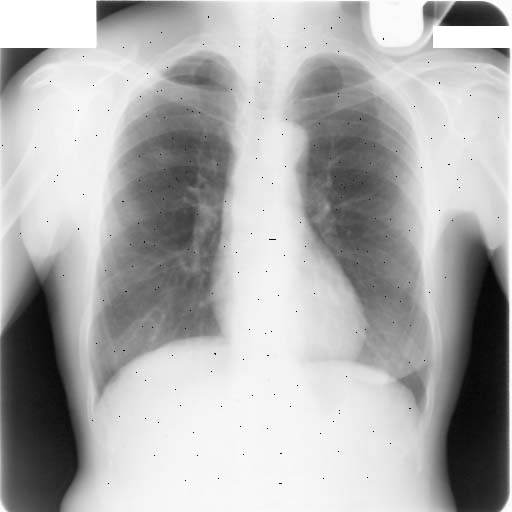
図3 スパイク雑音をのせた胸部X線画像
|
演習4-3:移動平均フィルタとメディアンフィルタを利用して画像中の雑音を除去してみよう! |
|
使用する画像:
図3の雑音をのせた胸部X線画像(Tif形式)
方法(移動平均フィルタ):
方法(メディアンフィルタ):
考察:
|
【微分フィルタによる濃度勾配の抽出】
微分は,数学的には関数の変化分をとりだす演算である.
この微分演算を画像に適用すれば,濃度値が急激に変化している部分を抽出することができる.
微分には,1次微分(グラディエント)と2次微分(ラプラシアン)がある.
ディジタル画像ではデータが一定間隔にとびとびに並んでいるため,本当の意味での微分演算はできない.
このため,隣接画素同士の差をとる演算で微分を近似し,これを”差分”という.
つまり,ディジタル画像において”微分”と表現される操作は,実際は差分演算を行うことになる.
画像に対する1次微分処理は,注目画素の周辺の勾配(傾き:グラディエント)と求める操作である.
この勾配は,大きさと方向をもつベクトル量であり,画像上ではさまざまは方向に勾配が存在していることがわかる.
そのため,1次微分では微分の方向によって結果が異なる.図4を見てみよう.
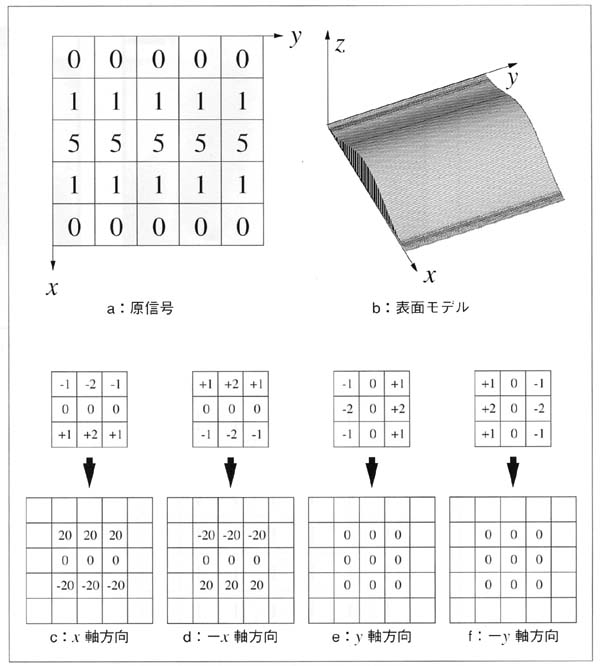
図4 たたみ込みによる微分と方向による結果の違い
aは原信号,bはその表面モデルである.
c~fはそれぞれ +x方向,-x方向,+y方向,-y方向を持つ微分カーネルを原画像にたたみ込んだ結果である.
この微分カーネルは,特にソーベルフィルタと呼ばれており,代表的な1次微分フィルタのひとつである.
そのほかの1次微分フィルタとして,Robertsフィルタ,Prewittフィルタなどがある.
さて,原信号ではx軸方向に傾きが存在するため,+x方向の傾きを検出するフィルタと-x方向の傾きを検出するフィルタを原信号にたたみ込んだ結果は,cとdのようになる.
一方,+y方向の傾きを検出するフィルタと-y方向の傾きを検出するフィルタを使用したeとfでは,原信号にy軸方向の傾きが存在しないため,すべての出力値が0となっている.
|
演習4-4:ソーベルフィルタを使った画像の1次微分処理を実践してみよう! |
|
使用する画像:
胸部X線画像
方法:
考察:
|
一方,2次微分はグラディエントをもう一度微分したもので,濃度勾配の強さだけ(向きは求められない)を検出するのに用いられる.
2次微分を行うカーネルを特にラプラシアンフィルタ(2次微分フィルタ)と呼ぶ.
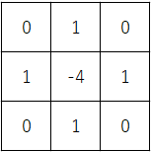
3×3のラプラシアンフィルタ(4近傍)
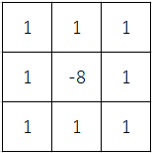
3×3のラプラシアンフィルタ(8近傍)
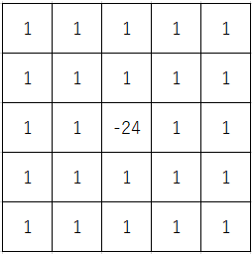
5×5のラプラシアンフィルタ
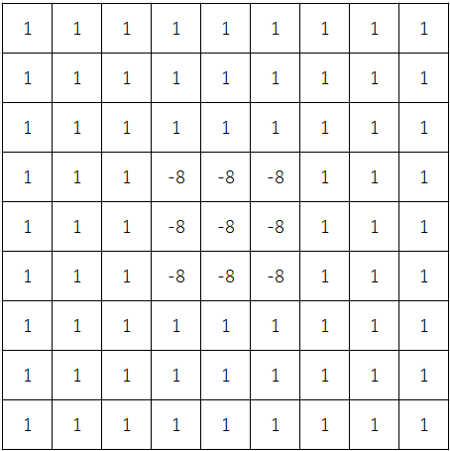
9×9のラプラシアンフィルタ
|
演習4-5:たたみ込みによる2次微分を実行してみよう! |
|
使用する画像:
胸部X線画像
方法:
考察:
|