図1 アナログ信号のデジタル化概要
【概要】
医用画像には,CTやMRIのようなデジタル撮影装置を利用して撮影されるデジタル画像と,X線フィルムに代表されるアナログ画像がある.
アナログ画像をコンピュータで解析するためにはデジタル化(=A/D変換:Analog-to-Digital conversion)を行わなければならない.
デジタル化の基本原理は,”標本化”と”量子化”で成りたっている.
最初に標本化を行い,その後に量子化を行う.この順番を入れ替えることはできない.
画像において, 標本化は空間分解能を,量子化は濃度分解能を決定する.
図1に,アナログ信号をデジタル化する方法の概要を,一次元的に簡単に示す.

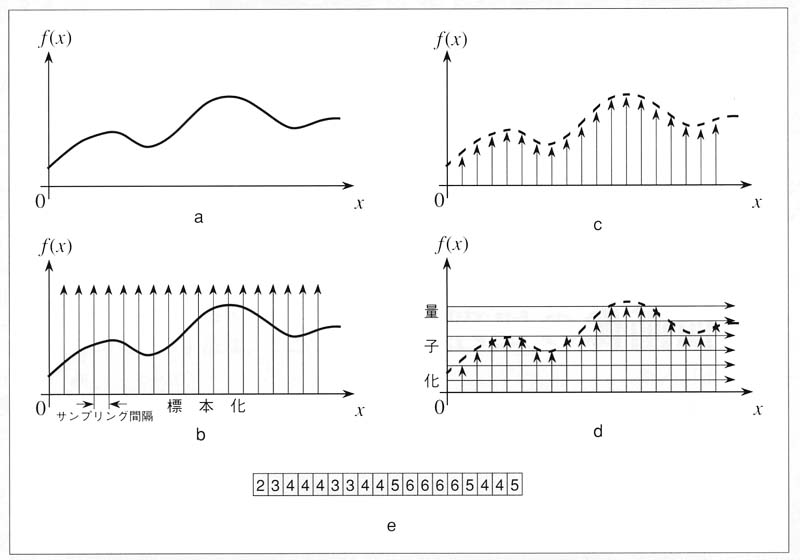
図1 アナログ信号のデジタル化概要
a:原信号,b:標本化操作,c:標本化後の”半デジタル信号” 横軸方向はデジタルであるが,縦軸方向はアナログの状態.
d:量子化操作,e:デジタル化の結果.
まず,原信号aをある一定間隔(サンプリング間隔)ごとに標本化を行う(b,c).
これは,信号の横軸方向(位置情報)のデジタル化の操作である.
次にその高さ(振幅情報)を量子化する(d).
これは連続値である原信号の振幅値(画像においては濃度値,輝度値に相当)を整数値(画素値に相当)に変換することである.
そして,最終的にその値を保存して,デジタルのデータを得る(e).
図2に,二次元画像のデジタル化の概要を示す.
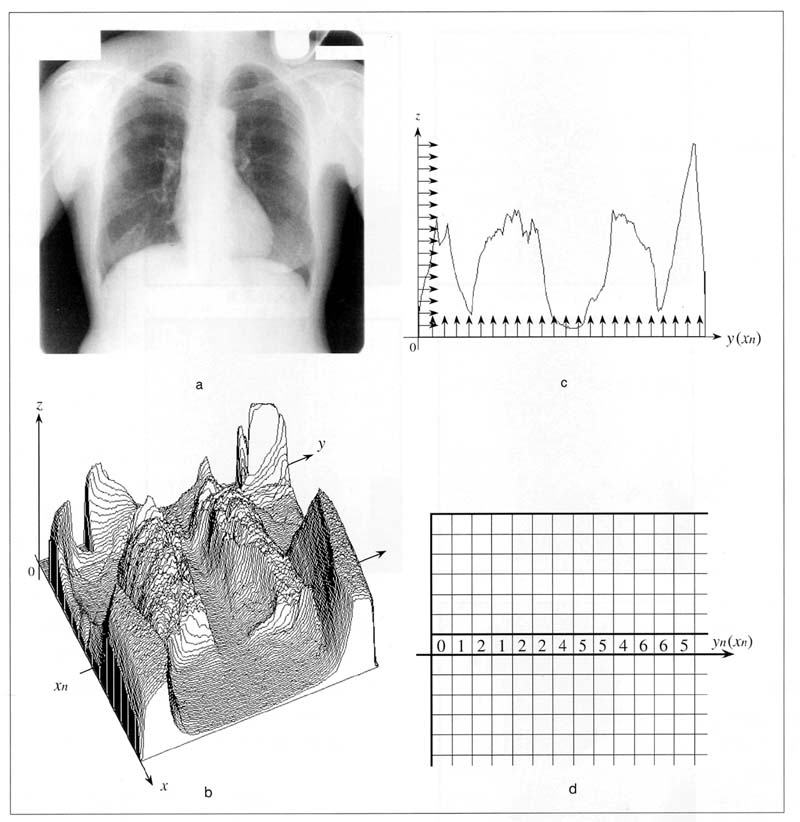
図2 二次元画像のデジタル化概要
a:原画像,b:垂直方向(ここでは,x方向)のデジタル化,
c:ある水平方向(ここでは,xにおけるy方向)のデジタル化,d:cの結果
b~dの操作を繰り返すことによって,画像のデジタル化が実行される.
二次元信号である画像をデジタル化するには,まず垂直方向と水平方向の2方向について標本化を行い,その後量子化を行う.
原画像aを垂直方向(x軸)にまず標本化し,その濃度をz軸方向の高さで表した結果がbである.
たくさんの水平方向のプロファイルで画像表現されていることがわかる.
cは,その水平方向のプロファイルのひとつ[y (xn )]を抽出して表示したものである.
このプロファイルに対し図1で示した標本化と量子化を行うことで,dに示すような整数値を得ることができる.
この操作を垂直方向に繰り返し行うことによって,画像全体をデジタル化することができる.
dにおいて,整数値が入っている四角のそれぞれを画素(ピクセル)と言い,その値を画素値(ピクセル値)と言う.
その総数を画素数と言い,これは原画像サンプリング間隔と原画像の大きさによって決定する.
また,画素数はデジタル画像のデータ量に比例する.
【標本化】
標本化処理では,被写体情報をどの程度の細かさでデジタル化するかが重要となる.
サンプリング間隔を小さくすれば小さい対象までデジタル化することができるが,画素数が多くなるためデータ量は増加する.
一般的には,サンプリング間隔の大きさは,ピクセル寸法(画素寸法)で表す.
ピクセル寸法とは, フィルム上でどのくらいの大きさの微小な四角形の領域をデジタル画像の1画素にしたかという意味である.
例えば「1ピクセル0.2mmでスキャンした画像」などと表現される.
また,このサンプリング間隔は,空間周波数(以下,単に周波数」としても表現することができる.
「1ピクセル0.2mm」は,周波数では,その逆数で計算される5cycles/mmと表され,サンプリング周波数と呼ばれる.
これは1mm間を5等分して標本化するということを意味している.
|
演習1-1: |
|
使用する画像: 胸部X線画像(chest.tif,512×512画素,8ビット,Tif形式) 方法:
考察:
|
サンプリング間隔により,デジタルで表現できる最小の大きさを決定することができる.
では, どのくらいのサンプリング間隔で標本化すれば,原信号の情報を損失なく表現できるだろうか.
その答えは”サンプリング(標本化)定理”にある.
標本化定理: 原信号をデジタルで完全に再現するためには,原信号の持つ最大の周波数の2倍以上の周波数で標本化する必要がある.
標本化定理を式で表すと次のようになる.
⊿t ≦ 1/2 fc (⊿t :標本化間隔, fc :原信号の持つ最大周波数)
上式で等号の成立する周波数
(fn) を特にナイキスト周波数と呼ぶ.
標本化定理から逆に考えると,アナログ信号をデジタル化する場合,サンプリング周波数の半分の周波数までしか再現できないことを意味する.
ここで,2つの異なった周期を持つ正弦波を3つの異なったサンプリング間隔でデジタル化した例を図3に示す.
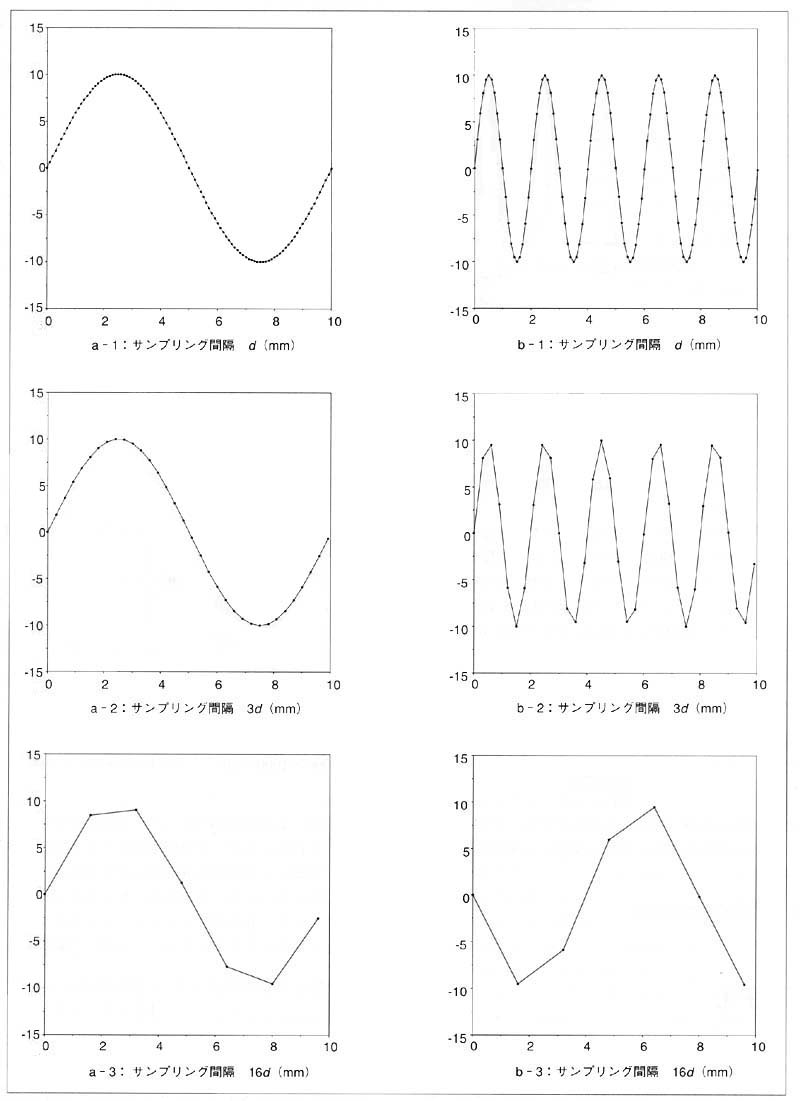
図3 周波数の異なる正弦波のデジタル化(d:サンプリングの数が100のときのサンプリング間隔)
aは,bと比較して低周波な正弦波であるため,サンプル数を少なくしても,a-1の波形の形状をほぼ表している.
しかし,bはサンプル数が少なくなるにつれて,b-1の形状から変化し,もとの信号にはない成分が現れてくる.
特に,b-3ではb-1の形状を予測することはとてもできない.
このように,サンプリング間隔を大きくしていくと,もとの信号にはない歪み(模様)が現れてくる.
このような歪みをエイリアシングと呼ぶ.
エイリアシングは,別の言い方をすると,高い周波数のものを低い周波数のものに見誤る現象である.
例えば,車のタイヤや扇風機の羽が高速に回転(高い周波数)しているとき,回転方向とは逆方向にゆっくり回転(低い周波数)しているかのように見える現象も一種のエイリアシングである.
同様の現象は画像のデジタル化においても確認できる.特に画像におけるエイリアシングは,モアレと呼ばれることもある.
|
演習1-2:サンプリング周波数を変えるとエイリアシングが現れることを確認してみよう! |
|
使用する画像: 同心円チャート画像, シーメンスチャート画像 方法:
考察:
|
【量子化】
量子化処理は,信号の振幅(画像においては”濃度”,”輝度”に相当)をデジタル化する処理である.
量子化の程度を表す尺度を”量子化レベル数”(=グレイレベル数 or 階調数)という.
量子化レベル数は,量子化の際に用いられるA/D変換器のビット数に依存する.
8ビットの変換器を用いた場合,8ビット=256階調で量子化するため,量子化レベル数は256になる.
一般的に,画像において階調数が2のG乗であるとき,Gビット量子化という.
Gの値が大きい(量子化レベル数が大きい)ほど,濃度分解能が良くなる.
量子化時に発生するアナログ信号とデジタル信号の差を”量子化誤差”と言う.
一般的に,量子化レベル数を増加させると,量子化誤差は小さくなる.
逆に量子化レベル数が小さくなると,量子化誤差が増加する.
画像においては,量子化レベル数が極端に小さくなると,本来存在しない疑似輪郭が現れる.
通常8ビット(256レベル)程度の階調数を用いれば人間の目には不自然さはない.
しかし, 医用X線画像をデジタル化する場合は,量子化レベル数を10ビット(1024レベル)~12ビット(4096)とすることがことがほとんどである.
これは,フィルムの光学的濃度は0から4.0近くに及ぶことがあり,8ビット程度の情報量では不充分である場合が多いからである.
|
演習1-3:量子化レベル数の違いが及ぼす画質への影響を確認してみよう! |
|
使用する画像: 胸部X線画像 同心円チャート画像, シーメンスチャート画像 方法:
考察:
|
【デジタル画像のデータ量】
デジタル画像のデータ量は,標本化におけるサンプリング間隔と,量子化における量子化レベル数で決定される.
胸部X線撮影で得られた10cm×10cmのフィルムをデジタル化することを例に,デジタル画像のデータ量を計算してみよう.
デジタル化の条件は,①サンプリング間隔:0.1mm(10cycles/mm),②量子化レベル数:1024(10ビット)とする.
まず,サンプリング間隔からデジタル画像の画素数(マトリックス数)が決定されるが,この場合は縦横とも10cmをサンプリング間隔0.1mmで標本化するため,縦横の画素数はそれぞれ1000画素になる.
また,量子化レベル数が1024=10ビットであることから,1画素が10ビットのデータ量を持つため,画像全体では,以下のようになる.
1000×1000×10ビット=10000000ビット
これはおよそ1メガバイト(3.5インチフロッピーディスク1枚分)のデータ量である.
しかしながら,コンピュータではデータの最小単位を8ビット=1バイトで扱われるため,この場合,量子化レベル数が10ビットであっても,1画素は2×8=16ビット必要となることに注意する必要がある.
このことを考慮すると,この場合の画像データ量は,以下のようになる
1000×1000×16ビット=16000000ビット=2000000バイト=1953.125キロバイト≒1.9メガバイト
また,より高精細な画像を得ようと考え,サンプリング間隔を半分にしてデジタル化を行うと,画素数は2000×2000画素となる.
つまり, データ量は,2000×2000×16ビット=64000000ビット=8000000バイト=7812.5キロバイト≒7.6メガバイトとなる.
これは1000×1000の場合の4倍のデータ量である.データ量は,サンプリング間隔の逆2乗に比例して増加する.
*) 1byte(バイト:B) = 8 bit(ビット), 1KB(キロバイト)= 1024B, 1MB(メガバイト)= 1024KB
|
チャレンジ:デジタル画像のデータ量を計算してみよう! |